Question

18．已知f（x）=ax²+bx+c，f（0）=2，f（1）=0，f（-1）=6
（1）求f（x）的解析式
（2）求f（x）的定义域，值域
（3）画出f（x）的图象．

Answer 1

分析 （1）根据f（0）=2，f（1）=0，f（-1）=6列出方程组，解出a，b，c的值；
（2）将函数解析式配方化成顶点式，结合开口方向得出值域；
（3）确定对称轴和顶点坐标，找到函数零点，作出图象．

解答 解：（1）∵f（0）=2，f（1）=0，f（-1）=6
∴$\left\{\begin{array}{l}{c=2}\\{a+b+c=0}\\{a-b+c=6}\end{array}\right.$，
解得a=1，b=-3，c=2．
∴f（x）=x²-3x+2．
（2）f（x）的定义域是R，
∵f（x）=x²-3x+2=（x-$\frac{3}{2}$）²-$\frac{1}{4}$≥-$\frac{1}{4}$，
∴f（x）的值域是[-$\frac{1}{4}$，+∞）．
（3）f（x）的图象为：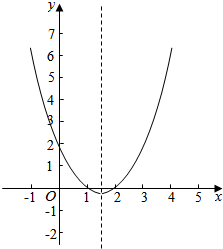

点评 本题考查了二次函数解析式的求法，值域及函数图象，是基础题．