题目内容
2.已知空间两不同直线m,n,两不同平面α、β,下列命题正确的是( )| A. | 若m∥α且n∥α,则m∥n | B. | 若m⊥β且m⊥n,则n∥β | ||
| C. | 若m⊥α且m∥β,则α⊥β | D. | 若α⊥β且m⊥α,m⊥n则n⊥β |
分析 根据空间线面位置关系的定义及判定定理或结合图形,给出反例进行判断.
解答 解:对于A,若m∥α且n∥α,则m与n可能平行,可能相交也可能异面,故A错误;
对于B,若n?β,显然结论错误;
对于C,若m∥β,则β内存在直线l使得l∥m,又m⊥α,故l⊥α,又l?β,故α⊥β,故C正确;
对于D,当n?β时,显然结论错误.
故选C.
点评 本题考查了空间位置关系的判断,属于中档题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
12.已知全集U=R,集合A={x|-3≤x≤1},集合B=$\left\{{x\left|{{2^x}<\frac{1}{4}}\right.}\right\}$,则A∩(∁UB)=( )
| A. | {x|-2<x<1} | B. | {x|-3≤x<-2} | C. | {x|-2≤x≤1} | D. | {x|-3≤x≤-2} |
11.设集合A={y|y=2x,-1<x<2},B={x|(x-1)(x+2)<0},则A∩B=( )
| A. | (-2,3) | B. | (-2,1) | C. | $(\frac{1}{2},2)$ | D. | $(\frac{1}{2},1)$ |
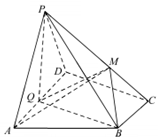 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD丄底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD,BC=$\frac{1}{2}$AD
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD丄底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD,BC=$\frac{1}{2}$AD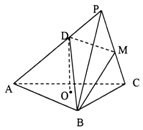 如图,三棱锥P-ABC中,底面ABC为等边三角形,O为△ABC的中心,平面PBC⊥平面ABC,PB=PC=BC=$\sqrt{3}$,D为AP上一点,且AD=2DP.
如图,三棱锥P-ABC中,底面ABC为等边三角形,O为△ABC的中心,平面PBC⊥平面ABC,PB=PC=BC=$\sqrt{3}$,D为AP上一点,且AD=2DP.