题目内容
对于实数x,试确定(
)-(
)的取值范围.
| x2+x+1 |
| x2-x+1 |
考点:函数的值域
专题:
分析:由已知可得(
)-(
)表示x轴上动点(x,0)到(-
,
)和(
,
)点的距离之差,由(-
,
)和(
,
)两点之间的距离为1,可得|(
)-(
)|<1,进而得到答案.
| x2+x+1 |
| x2-x+1 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| x2+x+1 |
| x2-x+1 |
解答:
解:∵(
)-(
)=
-
表示x轴上动点(x,0)到(-
,
)和(
,
)点的距离之差,
由(-
,
)和(
,
)两点之间的距离为1,
故|(
)-(
)|<1,
即-1<(
)-(
)<1,
故(
)-(
)的取值范围为(-1,1)
| x2+x+1 |
| x2-x+1 |
(x+
|
(x-
|
表示x轴上动点(x,0)到(-
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
由(-
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
故|(
| x2+x+1 |
| x2-x+1 |
即-1<(
| x2+x+1 |
| x2-x+1 |
故(
| x2+x+1 |
| x2-x+1 |
点评:本题考查的知识点是函数的值域,其中分析出(
)-(
)的几何意义,是解答的关键.
| x2+x+1 |
| x2-x+1 |

练习册系列答案
相关题目
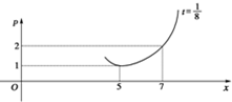 我国加入WTO时,根据达成的协议,若干年内某产品市场供应量p与关税的关系近似满足p(x)=2(1-kt)(x-b)2(其中t为关税的税率,且t∈[0,
我国加入WTO时,根据达成的协议,若干年内某产品市场供应量p与关税的关系近似满足p(x)=2(1-kt)(x-b)2(其中t为关税的税率,且t∈[0,