讨论函数y=ex+(a-1)x的单调区间．题目和参考答案——青夏教育精英家教网——

题目内容

11．讨论函数y=e^x+（a-1）x的单调区间．

分析求出函数的导数，通过讨论a的范围，从而求出函数的单调区间即可．

解答解：y′=e^x+a-1，
a≥1时，y′＞0，函数在R递增，
a＜1时，令y′＞0，解得：x＞ln（1-a），令y′＜0，解得：x＜ln（1-a），
∴函数在（-∞，ln（1-a））递减，在（ln（1-a），+∞）递增．

点评本题考查了函数的单调性问题，考查导数的应用，是一道基础题．

练习册系列答案

时刻准备着暑假作业原子能出版社系列答案

学生暑假实践手册北京出版社系列答案

新活力总动员寒假系列答案

暑假衔接教材期末暑假预习武汉出版社系列答案

假期作业暑假成长乐园新疆青少年出版社系列答案

学年复习王时代文艺出版社系列答案

期末暑假提优计划江苏人民出版社系列答案

暑假学习园地河南人民出版社系列答案

暑假假期集训白山出版社系列答案

世纪金榜新视野暑假作业系列答案

相关题目

1．在直角坐标系xOy中，以O为极点，x轴的正半轴为极轴建立极坐标系．已知直线l的极坐标方程为ρsinθ=1，曲线C的参数方程为$\left\{\begin{array}{l}x=2cosϕ\\ y=2sinϕ\end{array}\right.$（ϕ为参数），l与C相交于A，B两点，则|AB|=2$\sqrt{3}$．

2．设f（x）是定义域为R且最小正周期为2π的函数，且有f（x）=$\left\{\begin{array}{l}{sinx，0≤x≤π}\\{cosx，-π＜x＜0}\end{array}\right.$，则f（-$\frac{13π}{4}$）=（　　）

$\frac{\sqrt{2}}{2}$

-$\frac{\sqrt{2}}{2}$

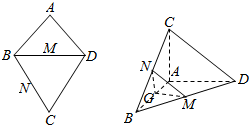如图，AB=AD，∠BAD=90°，M，N，G分别是BD，BC，AB的中点，将等边△BCD沿BD折叠到△BC′D的位置，使得AD⊥C′B．
（Ⅰ）求证：平面GNM∥平面ADC′；
（Ⅱ）求证：C′A⊥平面ABD．

6．在直角坐标系xOy中，圆C的参数方程为$\left\{\begin{array}{l}{x=2cosφ}\\{y=-2+2sinφ}\end{array}\right.$（φ为参数），以O为极点，x轴的非负半轴为极轴建立极坐标系．
（I）求圆C的极坐标方程；
（Ⅱ）若直线l的极坐标方程是ρcos（θ+$\frac{π}{4}$）=$\sqrt{2}$，求直线l被圆C截得的弦长．

16．已知函数f（x）=x³-ax-1．
（1）是否存在a．使f（x）的单调减区间是（-1，1）？
（2）若f（x）在R上是增函数．求a的取值范围．

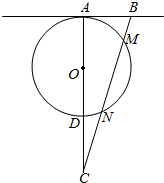如图所示，AD是⊙O的直径，AB是⊙O的切线，直线BMN交AD的延长线于点C，BM=MN=NC，AB=2，求CD的长和⊙O的半径．

20．在如下程序框图中，已知f₀（x）=sinx，则输出的结果是（　　）

1．已知x＞0，当x+$\frac{4}{x}$取最小值时x的值为2．