题目内容
定义在R上的可导函数f(x)=
x3+
ax2+2bx+c,当x∈(0,1)时取得极大值,当x∈(1,2)时,取得极小值,若(1-t)a+b+t-3>0恒成立,则实数t的取值范围为( )
| 1 |
| 3 |
| 1 |
| 2 |
| A、(2,+∞) | ||
| B、[2,+∞) | ||
C、(-∞,
| ||
D、(-∞,
|
考点:利用导数研究函数的极值,简单线性规划的应用
专题:导数的综合应用,不等式的解法及应用
分析:据极大值点左边导数为正右边导数为负,极小值点左边导数为负右边导数为正得a,b的约束条件,据线性规划求出最值.
解答:
 解∵f(x)=
解∵f(x)=
x3+
ax2+2bx+c,
∴f′(x)=x2+ax+2b,
∵函数f(x)在区间(0,1)内取得极大值,在区间(1,2)内取得极小值,
∴f′(x)=x2+ax+2b=0在(0,1)和(1,2)内各有一个根,
f′(0)>0,f′(1)<0,f′(2)>0,
即
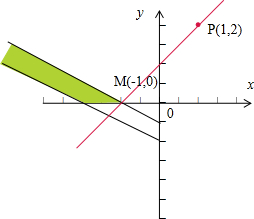
,在aOb坐标系中画出其表示的区域(不包括边界),如图:
若(1-t)a+b+t-3>0恒成立,可知a+b-3>t(a-1)恒成立,由可行域可知a<0,
可得t>
=1+
它的几何意义是表示点P(1,2)与可行域内的点A连线的斜率加1,
当A(x,y)位于M(-1,0)时,
最小,最小值为1;
则最小值为1+1=2,
∴
的取值范围[2,+∞),
故选:B.
 解∵f(x)=
解∵f(x)=| 1 |
| 3 |
| 1 |
| 2 |
∴f′(x)=x2+ax+2b,
∵函数f(x)在区间(0,1)内取得极大值,在区间(1,2)内取得极小值,
∴f′(x)=x2+ax+2b=0在(0,1)和(1,2)内各有一个根,
f′(0)>0,f′(1)<0,f′(2)>0,
即
|
若(1-t)a+b+t-3>0恒成立,可知a+b-3>t(a-1)恒成立,由可行域可知a<0,
可得t>
| a+b-3 |
| a-1 |
| b-2 |
| a-1 |
当A(x,y)位于M(-1,0)时,
| b-2 |
| a-1 |
则最小值为1+1=2,
∴
| a+b-3 |
| a-1 |
故选:B.
点评:考查学生利用导数研究函数极值的能力,以及会进行简单的线性规划的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知tanθ=2,则2sin2θ+sinθcosθ-cos2θ=( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知i是虚数单位,若复数z满足(z-i)(3-i)=10,则复数z所对应的点位于复平面的( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知双曲线
-
=1(a>0,b>0)的左、右焦点分别为F1,F2,P为双曲线上任一点,且
•
最小值的取值范围是[-
c2,-
c2],则该双曲线的离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
| 3 |
| 4 |
| 1 |
| 2 |
A、(1,
| ||
B、[
| ||
C、(1,
| ||
| D、[2,+∞) |
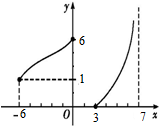 函数y=f(x)的图象如图所示,则函数y=f(x)的定义域为
函数y=f(x)的图象如图所示,则函数y=f(x)的定义域为