题目内容
16.若正实数a,b满足(2a+b)2=1+6ab,则$\frac{ab}{2a+b+1}$的最大值为$\frac{1}{6}$.分析 正实数a,b满足(2a+b)2=1+6ab,可得ab=$\frac{(2a+b)^{2}-1}{6}$,由(2a+b)2=1+6ab≤1+$3×(\frac{2a+b}{2})^{2}$,解得2a+b≤2.于是$\frac{ab}{2a+b+1}$=$\frac{(2a+b)^{2}-1}{6(2a+b)+6}$=$\frac{2a+b-1}{6}$,即可得出.
解答 解:∵正实数a,b满足(2a+b)2=1+6ab,
∴ab=$\frac{(2a+b)^{2}-1}{6}$.
∵(2a+b)2=1+6ab≤1+$3×(\frac{2a+b}{2})^{2}$,
解得2a+b≤2.当且仅当b=2a=1取等号.
则$\frac{ab}{2a+b+1}$=$\frac{(2a+b)^{2}-1}{6(2a+b)+6}$=$\frac{2a+b-1}{6}$≤$\frac{2-1}{6}$=$\frac{1}{6}$,
∴$\frac{ab}{2a+b+1}$的最大值为$\frac{1}{6}$.
故答案为:$\frac{1}{6}$.
点评 本题考查了基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.如图是某几何体的三视图且a=b,则该几何体主视图的面积为( )
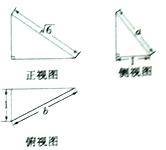

| A. | $\sqrt{6}$ | B. | $\frac{3}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{15}}}{2}$ |
4.已知曲线C1:y2=tx(y>0,t>0)在点M($\frac{4}{t}$,2)处的切线与曲线C2:y=ex+1-1也相切,则tln$\frac{4{e}^{2}}{t}$的值为( )
| A. | 4e2 | B. | 8e | C. | 2 | D. | 8 |
5.设U=R,M={y|y=2x+1,-$\frac{1}{2}$≤x≤$\frac{1}{2}$},N={x|y=lg(x2+3x)},则(∁UM)∩N=( )
| A. | (-∞,-3]∪(2,+∞) | B. | (-∞,-3)∪(0,+∞) | C. | (-∞,-3)∪(2,+∞) | D. | (-∞,0)∪(2,+∞) |
6.设$\overrightarrow{a}$,$\overrightarrow{b}$,是任意的非零平面向量,且相互不共线,则下列正确的是( )
| A. | 若向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|>|$\overrightarrow{b}$|,且$\overrightarrow{a}$,$\overrightarrow{b}$同向,则$\overrightarrow{a}$>$\overrightarrow{b}$ | |
| B. | |$\overrightarrow{a}$+$\overrightarrow{b}$|≤|$\overrightarrow{a}$|+|$\overrightarrow{b}$| | |
| C. | |$\overrightarrow{a}$•$\overrightarrow{b}$|≥|$\overrightarrow{a}$||$\overrightarrow{b}$| | |
| D. | |$\overrightarrow{a}$-$\overrightarrow{b}$|≤|$\overrightarrow{a}$|-|$\overrightarrow{b}$| |