题目内容
如图，在四棱锥P－ABCD中，AB∥CD，AB⊥AD，CD＝2AB，平面PAD⊥底面ABCD，PA⊥AD，E和F分别是CD、PC的中点，求证：
(1)PA⊥底面ABCD；
(2)BE∥平面PAD；
(3)平面BEF⊥平面PCD.
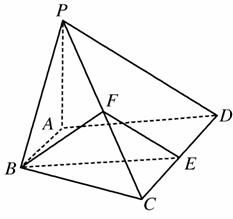
[解析] (1)因为平面PAD⊥底面ABCD，且PA垂直于这两个平面的交线AD，
所以PA⊥底面ABCD.
(2)因为AB∥CD，CD＝2AB，E为CD的中点，
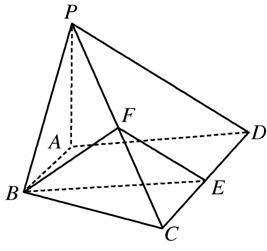
所以AB∥DE，且AB＝DE.
所以四边形ABED为平行四边形．
所以BE∥AD.
又因为BE平面PAD，AD平面PAD，
所以BE∥平面PAD.
(3)因为AB⊥AD，而且四边形ABED为平行四边形，
所以BE⊥CD，AD⊥CD.
由(1)知PA⊥底面ABCD.所以PA⊥CD.
所以CD⊥平面PAD.所以CD⊥PD.
因为E和F分别是CD和PC的中点，
所以PD∥EF.所以CD⊥EF，
又因为CD⊥BE，BE∩EF＝E，
所以CD⊥平面BEF.
所以平面BEF⊥平面PCD.
练习册系列答案
相关题目
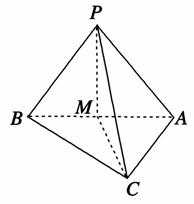
B．2
，则球O的表面积等于________．