题目内容
15.将y=sin2x+cos2x的图象向右平移$\frac{π}{4}$个单位后,所得图象的解析式是( )| A. | y=sin2x-cos2x | B. | y=cos2x-sin2x | C. | y=cos2x+sin2x | D. | y=cosxsinx |
分析 由条件利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:将函数y=sin2x+cos2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$)的图象向右平移$\frac{π}{4}$个单位后,
所得图象对应的解析式是y=$\sqrt{2}$sin[2(x-$\frac{π}{4}$)+$\frac{π}{4}$]=$\sqrt{2}$sin(2x-$\frac{π}{4}$)=sin2x-cos2x,
故选:A.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
20.在1,2,3,4四个数中随机地抽取一个数记为a,再在剩余的三个数中随机地抽取一个数记为b,则“$\frac{a}{b}$不是整数”的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
5.某商场举行优惠促销活动,顾客仅可以从以下两种优惠方案中选择一种,
方案一:每满200元减50元:
方案二:每满200元可抽奖一次.具体规则是依次从装有3个红球、1个白球的甲箱,装有2个红球、2个白球的乙箱,以及装有1个红球、3个白球的丙箱中各随机摸出1个球,所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
(Ⅰ)若两个顾客都选择方案二,各抽奖一次,求至少一个人获得半价优惠的概率;
(Ⅱ)若某顾客购物金额为320元,用所学概率知识比较哪一种方案更划算?
方案一:每满200元减50元:
方案二:每满200元可抽奖一次.具体规则是依次从装有3个红球、1个白球的甲箱,装有2个红球、2个白球的乙箱,以及装有1个红球、3个白球的丙箱中各随机摸出1个球,所得结果和享受的优惠如下表:(注:所有小球仅颜色有区别)
| 红球个数 | 3 | 2 | 1 | 0 |
| 实际付款 | 半价 | 7折 | 8折 | 原价 |
(Ⅱ)若某顾客购物金额为320元,用所学概率知识比较哪一种方案更划算?
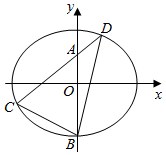 如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{3}$,点$(\sqrt{3},\sqrt{2})$为椭圆上的一点.
如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{3}$,点$(\sqrt{3},\sqrt{2})$为椭圆上的一点.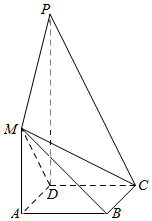 如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1.
如图,正方形ABCD与梯形AMPD所在的平面互相垂直,AD⊥PD,MA∥PD,MA=AD=$\frac{1}{2}$PD=1. 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,BC=3,BD=4,直线AD与平面BCD所成的角为45°,点E,F分别是AC,AD的中点.
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥BD,BC=3,BD=4,直线AD与平面BCD所成的角为45°,点E,F分别是AC,AD的中点.