题目内容
4．
如图，在三棱锥A-BCD中，AB⊥平面BCD，BC⊥BD，BC=3，BD=4，直线AD与平面BCD所成的角为45°，点E，F分别是AC，AD的中点．（1）求证：EF∥平面BCD；
（2）求三棱锥A-BCD的体积．
分析 （1）由中位线定理可得EF∥CD，故EF∥平面BCD；
（2）以BCD为底面，则棱锥的高为AB，代入体积公式计算即可．
解答 解：（1）∵点E，F分别是AC，AD的中点，
∴EF∥CD，又∵EF?平面BCD，CD?平面BCD，
∴EF∥平面BCD．
（2）∵AB⊥平面BCD，
∴∠ADB为直线AD与平面BCD所成的角，
∴∠ADB=45°，
∴AB=BD=4，
∵BC⊥BD，
∴S△BCD=$\frac{1}{2}×BC×BD$=6．
∴三棱锥A-BCD的体积V=$\frac{1}{3}{S}_{△BCD}•AB$=8．
点评 本题考查了线面平行的判定，棱锥的体积计算，属于基础题．
练习册系列答案
相关题目
15．将y=sin2x+cos2x的图象向右平移$\frac{π}{4}$个单位后，所得图象的解析式是（ ）
| A． | y=sin2x-cos2x | B． | y=cos2x-sin2x | C． | y=cos2x+sin2x | D． | y=cosxsinx |
12．命题“?a∈R，函数y=π”是增函数的否定是（ ）
| A． | “?a∈R，函数y=π”是减函数 | B． | “?a∈R，函数y=π”不是增函数 | ||
| C． | “?a∈R，函数y=π”不是增函数 | D． | “?a∈R，函数y=π”是减函数 |
9．
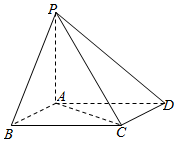如图，已知在四棱锥P-ABCD中，底面ABCD是菱形，PA⊥底面ABCD，AB=1，PA•AC=1，∠ABC=θ（0＜θ≤$\frac{π}{2}$），则四棱锥P-ABCD的体积V的取值范围是（ ）
如图，已知在四棱锥P-ABCD中，底面ABCD是菱形，PA⊥底面ABCD，AB=1，PA•AC=1，∠ABC=θ（0＜θ≤$\frac{π}{2}$），则四棱锥P-ABCD的体积V的取值范围是（ ）| A． | [$\frac{\sqrt{2}}{6}$，$\frac{1}{3}$） | B． | （$\frac{\sqrt{2}}{12}$，$\frac{1}{6}$] | C． | （$\frac{\sqrt{2}}{6}$，$\frac{1}{3}$] | D． | [$\frac{\sqrt{2}}{12}$，$\frac{1}{6}$） |
14．如图所示，使电路接通，开关不同的开闭方式共有（ ）
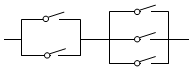
| A． | 11 | B． | 12 | C． | 20 | D． | 21 |