题目内容
9.已知点P是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)上的动点,F1,F2为椭圆的左右焦点,焦距为2c,O为坐标原点,若M是∠F1PF2的角平分线上的一点,且MF1⊥MP,则OM的取值范围为(0,c).分析 利用M是∠F1PF2平分线上的一点,且F1M⊥MP,判断OM是三角形F1F2N的中位线,把OM用PF1,PF2表示,再利用椭圆的焦半径公式,转化为用椭圆上点的横坐标表示,借助椭圆的范围即可求出OM的范围.
解答 解:如图,延长PF2,F1M,交与N点,∵PM是∠F1PF2平分线,且F1M⊥MP,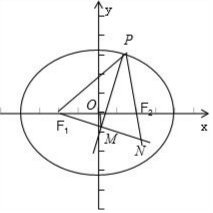
∴|PN|=|PF1|,M为F1N中点,
连接OM,∵O为F1F2中点,M为F1N中点
∴|OM|=$\frac{1}{2}$|F2N|=$\frac{1}{2}$||PN|-|PF2||=$\frac{1}{2}$||PF1|-|PF2||
∵在椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)中,设P点坐标为(x0,y0)
则|PF1|=a+ex0,|PF2|=a-ex0,
∴||PF1|-|PF2||=|a+ex0-a+ex0|=|2ex0|=2e|x0|
∵P点在椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)上,
∴|x0|∈(0,a],
又∵当|x0|=a时,F1M⊥MP不成立,∴|x0|∈(0,a)
∴|OM|∈(0,c).
故答案为:(0,c).
点评 本题考查了椭圆的定义标准方程及其性质、三角形中位线定理,考查了推理能力与计算能力,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.以下四个命题中不正确的是 ( )
| A. | $f(x)=\frac{|x|}{x}$是奇函数 | B. | f(x)=x2,x∈(-3,3]是偶函数 | ||
| C. | f(x)=(x-3)2是非奇非偶函数 | D. | y=x4+x2是偶函数 |
4.若$\overline z$=$\frac{i}{1+i}$,则z•$\overline z$=( )
| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{1}{2}$ |
1.已知A={(x,y)|y=x-3},B={(x,y)|y=-x-5},则A∩B为( )
| A. | {-1,4} | B. | {-1,-4} | C. | {(-1,4)} | D. | {(-1,-4)} |
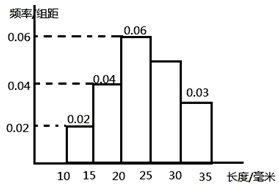 对一批产品的长度(单位:mm)进行抽样检测,如图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上的为一等品,在[15,20)和[25,30)上的为二等品,在[10,15)和[30,35)上的为三等品;
对一批产品的长度(单位:mm)进行抽样检测,如图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上的为一等品,在[15,20)和[25,30)上的为二等品,在[10,15)和[30,35)上的为三等品;