题目内容
设a,b∈R,i是虚数单位,则“ab=0”是“复数a+
为纯虚数”的 条件.
| b |
| i |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据复数的概念,利用充分条件和必要条件的定义进行判断.
解答:
解:复数a+
=a-bi,若复数a+
为纯虚数,则a=0且b≠0,
若ab=0,则a=0或b=0,此时充分性不成立,
若a=0且b≠0,则ab=0成立,即必要性成立,
则“ab=0”是“复数a+
为纯虚数”的必要不充分条件,
故答案为:必要不充分
| b |
| i |
| b |
| i |
若ab=0,则a=0或b=0,此时充分性不成立,
若a=0且b≠0,则ab=0成立,即必要性成立,
则“ab=0”是“复数a+
| b |
| i |
故答案为:必要不充分
点评:本题主要考查充分条件和必要条件的判断,根据复数的有关概念是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
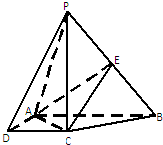 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,E是PB的中点.(1)求证:EC∥平面PAD
(2)求证:平面EAC⊥平面PBC.