题目内容
若数列{an}满足前n项之和Sn=2an-4(n∈N*),bn+1=an+2bn,且b1=2,
(1)求数列{an}的通项公式
(2)证明:{
}是等差数列
(3)求bn的前n项和Tn.
(1)求数列{an}的通项公式
(2)证明:{
| bn |
| 2n |
(3)求bn的前n项和Tn.
考点:数列的求和,等差关系的确定
专题:等差数列与等比数列
分析:(1)当n=1时,a1=S1=2a1-4可求a1=4,当n≥2时,由an=Sn-Sn-1=2an-4-2an-1+4即an=2an-1,可得an,
(2)bn+1=an+2bn,代入an可证,
(3)Tn=1×2+2×22+…+n•2n,考虑利用错位相减可求Tn.
(2)bn+1=an+2bn,代入an可证,
(3)Tn=1×2+2×22+…+n•2n,考虑利用错位相减可求Tn.
解答:
解:(1)当n=1时,a1=S1=2a1-4
∴a1=4
当n≥2时,an=Sn-Sn-1=2an-4-2an-1+4
即an=2an-1
∴
=2
∴an=2n+1,
(2)bn+1=2n+1+2bn
∴
-
=1
又
=
=1
∴
=1+(n-1)×1=n,
∴bn=n•2n(n∈N*)
(3)Tn=1×2+2×22+…+n•2n
2Tn=1×22+…+(n-1)•2n+n•2n+1
两式相减得 Tn=-2-22-…-2n+n•2n+1
=
+n•2n+1
=(n-1)•2n+1+2(n∈N*).
∴a1=4
当n≥2时,an=Sn-Sn-1=2an-4-2an-1+4
即an=2an-1
∴
| an |
| an-1 |
∴an=2n+1,
(2)bn+1=2n+1+2bn
∴
| bn+1 |
| 2n+1 |
| bn |
| 2n |
又
| b1 |
| 21 |
| 2 |
| 2 |
∴
| bn |
| 2n |
∴bn=n•2n(n∈N*)
(3)Tn=1×2+2×22+…+n•2n
2Tn=1×22+…+(n-1)•2n+n•2n+1
两式相减得 Tn=-2-22-…-2n+n•2n+1
=
| -2(1-2n) |
| 1-2 |
=(n-1)•2n+1+2(n∈N*).
点评:本题主要考查了利用数列的递推公式求解数列的通项公式,解题的关键是构造等差及等比数列进行求解,要注意对错位相减求解数列和的方法的掌握,这是数列求和中的重点和难点.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
复数(a2-a-2)+(|a-1|-1)i(a∈R)不是纯虚数,则有( )
| A、a≠0 | B、a≠2 |
| C、a≠0且a≠2 | D、a≠-1 |
集合A={x|x2-x-2<0},B={x||x|<1},则( )
| A、A?B | B、B?A |
| C、A=B | D、A∩B=∅ |
已知f(x)=Asin(ωx+φ)(A>0,ω>0)的一段图象如下,则f(x)的解析式为( )
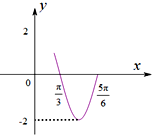

A、f(x)=2sin(2x+
| ||
B、f(x)=2sin(2x-
| ||
C、f(x)=2sin(2x+
| ||
D、f(x)=2sin(2x-
|
定义在R上的奇函数f(x),满足f(x)=f(x-3),f(-2)=0,则f(x)在区间(0,6)内零点个数( )
| A、至多4个 | B、至多5个 |
| C、恰好6个 | D、至少6个 |
 某公司从一批产品中随机抽出60件进行检测.如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].
某公司从一批产品中随机抽出60件进行检测.如图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].