题目内容
求函数f(x)＝2x＋lg(x＋1)－2的零点个数．
[解析] 解法一：∵f(0)＝1＋0－2＝－1＜0，f(2)＝4＋lg3－2＝2＋lg3＞0，
∴函数f(x)在区间(0,2)上必定存在零点．
又f(x)＝2x＋lg(x＋1)－2在区间(－1，＋∞)上为增函数，故函数f(x)有且只有一个零点．
解法二：在同一坐标系内作出函数h(x)＝2－2x和g(x)＝lg(x＋1)的图象，如图所示，由图象知y＝lg(x＋1)和y＝2－2x有且只有一个交点，即f(x)＝2x＋lg(x＋1)－2有且只有一个零点．
练习册系列答案
优生乐园系列答案
相关题目
B．
D．1
的定义域为R，则实数k的取值范围为( )
) B．(
B．y＝4－
(x≥0)
，已知到今年为止，森林剩余面积为原来的
.
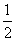}，则f(10x)>0的解集为( )
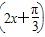＋sin2x.
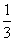，f(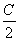
)＝－
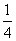，且C为锐角，求sinA的值．