题目内容
一片森林原来面积为a,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的 ,已知到今年为止,森林剩余面积为原来的
,已知到今年为止,森林剩余面积为原来的 .
.
(1)求每年砍伐面积的百分比.
(2)到今年为止,该森林已砍伐了多少年?
(3)今后最多还能砍伐多少年?
[解析] (1)设每年砍伐面积的百分比为x(0<x<1),则a(1-x)10=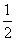 a,即(1-x)10=
a,即(1-x)10=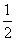 .
.
解得x=1-(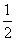 )
) .
.
(2)设经过m年剩余面积为原来的 ,则
,则
a(1-x)m= a,即(
a,即(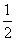 )
) =(
=(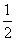 )
) ,
,
 =
=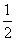 ,解得m=5.
,解得m=5.
故到今年为止,已砍伐了5年.
(3)设从今年开始,以后砍伐了n年,
则n年后剩余面积为 a(1-x)n.
a(1-x)n.
令 a(1-x)n≥
a(1-x)n≥ a,即(1-x)n≥
a,即(1-x)n≥ ,
,
(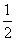 )
) ≥(
≥(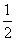 )
) ,
, ≤
≤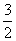 ,解得n≤15.
,解得n≤15.
故今后最多还能砍伐15年.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案图形ABC如图所示,为了求其面积,小明在封闭的图中找出了一个半径为1 m的圆,在不远处向圈内掷石子,且记录如下:

|
| 50次 | 150次 | 300次 |
| 石子落在⊙O内(含⊙O上)的次数m | 14 | 43 | 93 |
| 石子落在阴影内次数n | 29 | 85 | 186 |
则估计封闭图形ABC的面积为________m2.
已知函数f(x),g(x)分别由下表给出
| x | 1 | 2 | 3 |
| f(x) | 2 | 3 | 1 |
| x | 1 | 2 | 3 |
| g(x) | 3 | 2 | 1 |
则f[g(1)]的值为________;
当g[f(x)]=2时,x=________.
若函数f(x)=x3-x-1在区间[1,1.5]内的一个零点附近函数值用二分法逐次计算列表如下
| x | 1 | 1.5 | 1.25 | 1.375 | 1.3125 |
| f(x) | -1 | 0.875 | -0.2969 | 0.2246 | -0.05151 |
那么方程x3-x-1=0的一个近似根(精确度为0,1)为( )
A.1.2 B.1.3125
C.1.4375 D.1.25
已知函数f(x)的图像是连续不断的,x、 f(x)的对应关系如下表:
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| f(x) | 136.136 | 15.552 | -3.92 | 10.88 | -52.488 | -232.064 |
则函数f(x)存在零点的区间为( )
A.区间[1,2]和[2,3]
B.区间[2,3]和[3,4]
C.区间[2,3]和[3,4]和[4,5]
D.区间[3,4]和[4,5]和[5,6]

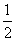
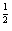 ,则a,b,c大小关系为______.
,则a,b,c大小关系为______. .
.