题目内容
函数f(x)=ax+b的零点是-1(a≠0),则函数g(x)=ax2+bx的零点是( )
A.-1 B.0
C.-1和0 D.1和0
C
[解析] 由条件知f(-1)=0,∴b=a,∴g(x)=ax2+bx=ax(x+1)的零点为0和-1.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
已知函数f(x),g(x)分别由下表给出
| x | 1 | 2 | 3 |
| f(x) | 2 | 3 | 1 |
| x | 1 | 2 | 3 |
| g(x) | 3 | 2 | 1 |
则f[g(1)]的值为________;
当g[f(x)]=2时,x=________.
若函数f(x)=x3-x-1在区间[1,1.5]内的一个零点附近函数值用二分法逐次计算列表如下
| x | 1 | 1.5 | 1.25 | 1.375 | 1.3125 |
| f(x) | -1 | 0.875 | -0.2969 | 0.2246 | -0.05151 |
那么方程x3-x-1=0的一个近似根(精确度为0,1)为( )
A.1.2 B.1.3125
C.1.4375 D.1.25
 B.
B.
 D.
D.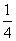
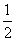 )ax,a为常数,且函数的图象过点(-1,2).
)ax,a为常数,且函数的图象过点(-1,2).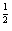 ,则a,b,c大小关系为______.
,则a,b,c大小关系为______. =________.
=________.