题目内容
12.下列各组函数中,表示相同的函数的是( )| A. | f(x)=x与g(x)=$\frac{{x}^{2}}{x}$ | B. | f(x)=|x|与g(x)=$\sqrt{{x}^{2}}$ | ||
| C. | f(x)=x0与g(x)=1 | D. | f(x)=$\sqrt{{x}^{2}-1}$与g(x)=$\sqrt{x-1}$$\sqrt{x+1}$ |
分析 根据相等函数的定义判断即可.
解答 解:对于A:f(x)的定义域是R,g(x)的定义域是{x|x≠0},不是同一函数,
对于B:f(x)=|x|与g(x)=$\sqrt{{x}^{2}}$=|x|,是同一函数,
对于C:f(x)的定义域是{x|x≠0},g(x)的定义域是R,不是同一函数,
对于D:f(x)=$\sqrt{{x}^{2}-1}$的定义域是:x≥1或x≤-1,
g(x)=$\sqrt{x-1}$$\sqrt{x+1}$的定义域是:{x|x≥1},不是同一函数,
故选:B.
点评 本题考查了相等函数的定义,分别判断其定义域、对应关系、值域即可.

练习册系列答案
相关题目
2.若cos2α=$\frac{\sqrt{2}}{3}$,则sin4α+cos4α的值为( )
| A. | 1 | B. | $\frac{7}{9}$ | C. | $\frac{11}{18}$ | D. | $\frac{13}{18}$ |
3.抛物线y=x2与直线x=0、x=1及该抛物线在x=t(0<t<1)处的切线所围成的图形面积的最小值为( )
| A. | $\frac{1}{12}$ | B. | $\frac{1}{10}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{4}$ |
17.等比数列{an}中,a2a4=$\frac{1}{2}$,则a1a32a5=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
1.已知函数y=Asin(ωx+φ)(x∈R)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,则( )
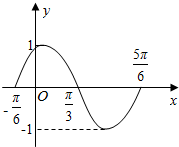

| A. | y=sin(x-$\frac{π}{6}$) | B. | y=sin(2x+$\frac{π}{3}$) | C. | y=-sin(2x+$\frac{π}{6}$) | D. | y=sin(2x+$\frac{π}{6}$) |