题目内容
11.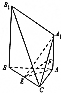 如图,已知A1A⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2$\sqrt{5}$,AA1=$\sqrt{7}$,BB1=2$\sqrt{7}$,点E和F分别为BC和A1C的中点.
如图,已知A1A⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2$\sqrt{5}$,AA1=$\sqrt{7}$,BB1=2$\sqrt{7}$,点E和F分别为BC和A1C的中点.(1)求证:EF∥平面A1B1BA;
(2)求证:平面AEA1⊥平面BCB1;
(3)求几何体ABCA1B1的体积.
分析 (1)连结A1B,根据中位线定理可得EF∥A1B,故而有EF∥平面A1B1BA;
(2)由A1A⊥平面ABC,BB1∥AA1可得B1B⊥平面ABC,故B1B⊥AE,由等腰三角形三线合一可得BC⊥AE,于是AE⊥平面B1BC,从而得出平面AEA1⊥平面BCB1;
(3)将几何体分解成两个小三棱锥A1-B1BC和A1-ABC求体积.
解答 证明:(1)连结A1B,在△A1BC中,
∵点E和F分别为BC和A1C的中点,
∴EF∥A1B,∵EF?平面平面A1B1BA,A1B?平面A1B1BA,
∴EF∥平面A1B1BA.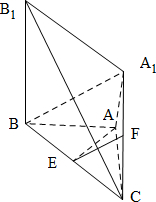
(2)∵AB=AC,E为BC的中点,∴AE⊥BC.
∵A1A⊥平面ABC,BB1∥AA1,
∴B1B⊥平面ABC,∵AE?平面ABC,
∴B1B⊥AE.又∵B1B?平面B1BC,BC?平面B1BC,B1B∩BC=B,
∴AE⊥平面B1BC,∵AE?平面AEA1,
∴平面AEA1⊥平面BCB1.
(3)∵AC=3,CE=$\frac{1}{2}BC=\sqrt{5}$,∴AE=$\sqrt{A{C}^{2}-C{E}^{2}}$=2.
∴三棱锥A1-B1BC的体积V1=$\frac{1}{3}×\frac{1}{2}×BC×{B}_{1}B×AE$=$\frac{1}{3}×\frac{1}{2}×2\sqrt{5}×2\sqrt{7}×2$=$\frac{4\sqrt{35}}{3}$.
三棱锥A1-ABC的体积V2=$\frac{1}{3}×\frac{1}{2}×BC×AE×\sqrt{7}$=$\frac{1}{3}×\frac{1}{2}×2\sqrt{5}×2×\sqrt{7}$=$\frac{2\sqrt{35}}{3}$.
∴几何体ABCA1B1的体积V=V1+V2=$\frac{4\sqrt{35}}{3}$+$\frac{2\sqrt{35}}{3}$=2$\sqrt{35}$.
点评 本题考查了线面垂直的性质,线面平行,面面垂直的判定,棱锥的体积计算,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | {x|x≥2} | B. | {x|x>-1} | C. | {x|x<2} | D. | {x|x<0} |
| A. | 命题p是真命题 | B. | 命题p的否命题是假命题 | ||
| C. | 命题p的逆否命题是假命题 | D. | 命题p的否命题是真命题 |
| A. | $y={(\sqrt{x+1})^2}$ | B. | $y=\root{3}{x^3}+1$ | C. | $y=\frac{x^2}{x}+1$ | D. | $y=\sqrt{x^2}+1$ |
| A. | 钝角三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 不能确定 |