题目内容
19.(1)求z=2x+y的最大值,使式中的x、y满足约束条件$\left\{\begin{array}{l}y≤x\\ x+y≤1\\ y≥-1.\end{array}\right.$(2)求z=2x+y的最大值,使式中的x、y满足约束条件$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1.
分析 (1)由题意作出可行域,从而利用线性规划求最大值;
(2)由题意作图象,从而可得当d有最大值时,|z|有最大值,即z有最值;从而结合图象解得.
解答 解:(1)由题意作出可行域如下,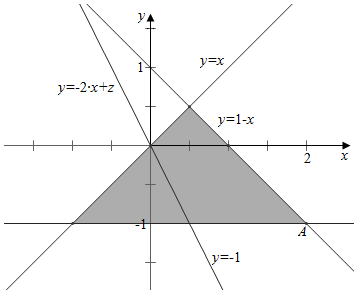 ,
,
结合图象可知,当过点A(2,-1)时有最大值,
故Zmax=2×2-1=3;
(2)由题意作图象如下,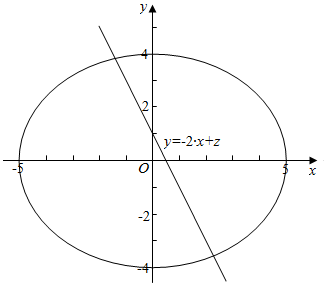 ,
,
根据距离公式,原点O到直线2x+y-z=0的距离d=$\frac{|z|}{\sqrt{5}}$,
故当d有最大值时,|z|有最大值,即z有最值;
结合图象可知,当直线2x+y-z=0与椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1相切时最大,
联立方程$\left\{\begin{array}{l}{\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1}\\{y=-2x+z}\end{array}\right.$化简可得,
116x2-100zx+25z2-400=0,
故△=10000z2-4×116×(25z2-400)=0,
故z2=116,
故z=2x+y的最大值为$\sqrt{116}$.
点评 本题考查了线性规划的应用及圆锥曲线与直线的位置关系的应用.

练习册系列答案
相关题目
10.已知定义在R上的奇函数f(x)满足f(x)=2x-4(x>0),则{x|f(x-1)>0}等于( )
| A. | {x|x>3} | B. | {x|-1<x<1} | C. | {x|-1<x<1或x>3} | D. | {x|x<-1} |
14.下列说法正确的是( )
| A. | 命题“p∨q”为真命题,则命题“p”和命题“q”均为真命题 | |
| B. | 已知x∈R,则“x>1”是“x>2”的充分不必要条件 | |
| C. | 命题“?x∈R,x2-x>0”的否定是:“?x∈R,x2-x≤0” | |
| D. | 命题“若am2<bm2,则a<b”的逆命题是真命题 |
4.“m>0”是“方程$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{m}$=1表示椭圆”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.乘积(x+y+z)(a-b+c)(m-n+p+q-3)展开后共有( )项.
| A. | 11 | B. | 12 | C. | 45 | D. | 120 |
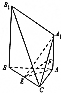 如图,已知A1A⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2$\sqrt{5}$,AA1=$\sqrt{7}$,BB1=2$\sqrt{7}$,点E和F分别为BC和A1C的中点.
如图,已知A1A⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2$\sqrt{5}$,AA1=$\sqrt{7}$,BB1=2$\sqrt{7}$,点E和F分别为BC和A1C的中点.