题目内容
16.$\frac{3-sin70°}{2-cos{\;}^{2}10°}$=2.分析 利用诱导公式、二倍角的余弦公式,求得所给式子的值.
解答 解:$\frac{3-sin70°}{2{-cos}^{2}10°}$=$\frac{3-cos20°}{2-\frac{1+cos20}{2}}$=$\frac{3-cos20°}{\frac{3-cos20°}{2}}$=2,
故答案为:2.
点评 本题主要考查诱导公式、二倍角的余弦公式的应用,属于基础题.

练习册系列答案
相关题目
6.阅读如图所示的程序框图,输入的s值为( )


| A. | 0 | B. | $1+\sqrt{2}$ | C. | $1+\frac{{\sqrt{2}}}{2}$ | D. | $\sqrt{2}-1$ |
7.△ABC的三内角A,B,C所对边的长分别是a,b,c,若$\frac{sinB-sinA}{sinC}=\frac{{\sqrt{2}a+c}}{a+b}$,则角B的大小为( )
| A. | $\frac{π}{4}$ | B. | $\frac{3π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
4.设$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$均为非零向量,已知命题p:$\overrightarrow{a}$=$\overrightarrow{b}$是$\overrightarrow{a}$•$\overrightarrow{c}$=$\overrightarrow{b}$•$\overrightarrow{c}$的必要不充分条件,命题q:x>1是|x|>1成立的充分不必要条件,则下列命题是真命题的是( )
| A. | p∧q | B. | p∨q | C. | (¬p)∧(¬q) | D. | p∨(¬q) |
1.用1,2,3,4,5这5个数字,组成无重复数字的三位数,其中奇数有( )
| A. | 12种 | B. | 24种 | C. | 36种 | D. | 48种 |
5.在复平面内,复数z的对应点为(1,-1),则z2=( )
| A. | $\sqrt{2}$ | B. | $-\sqrt{2}$ | C. | 2i | D. | -2i |
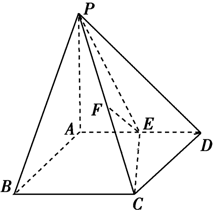 如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AD=2,E、F分别为棱AD、PC的中点.
如图所示,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AD=2,E、F分别为棱AD、PC的中点.