题目内容
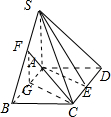
 如图,在四棱锥S-ABCD中,SA=AB=2,SB=SD=2
如图,在四棱锥S-ABCD中,SA=AB=2,SB=SD=2| 2 |
且∠ABC=60°,E为CD的中点.
(1)证明:CD⊥平面SAE;
(2)侧棱SB上是否存在点F,使得CF∥平面SAE?并证明你的结论.
考点:直线与平面平行的性质,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)根据线面垂直的判定定理,只要证明CD垂直于平面SAE内的两条相交直线即可,容易证明CD⊥AE,CD⊥SA,所以会得到CD⊥平面SAE.
(2)要找直线CF∥平面SAE,转化为找CF所在的平面和平面SAE平行,分别作两条直线和平面SAE内的两直线平行,这样能得到一个平面和SAE平面平行,取AB中点G,连接CG,过G作GF∥SA,交SB于F,容易证明平面CFG∥平面SAE,所以CF∥平面SAE,这样F点就找到了.
(2)要找直线CF∥平面SAE,转化为找CF所在的平面和平面SAE平行,分别作两条直线和平面SAE内的两直线平行,这样能得到一个平面和SAE平面平行,取AB中点G,连接CG,过G作GF∥SA,交SB于F,容易证明平面CFG∥平面SAE,所以CF∥平面SAE,这样F点就找到了.
解答:
解:(1)∵SA=AB=2,SB=2
,∴∠SAB=90°;∵底面ABCD是菱形,∴AB=AD,同理可得∠SAD=90°;
 ∴SA⊥AB,SA⊥AD;
∴SA⊥AB,SA⊥AD;
∴SA⊥平面ABCD,CD?平面ABCD;
∴SA⊥CD,即CD⊥SA;
连接AC,∠ADC=60°,AD=CD;
∴△ACD为等边三角形,∴AE⊥CD,即CD⊥AE;
∴CD⊥平面SAE.
(2)取AB中点G,并过G作GF∥SA,交SB于F,连接CF;
∵CG∥AE,AE?平面SAE,CG?平面SAE;
∴CG∥平面SAE,同理可得FG∥平面SAE,FG∩CF=G;
∴平面CFG∥平面SAE,CF?平面CFG;
∴CF∥平面SAE,并且F为SB的中点.
这样就找到了点F.
| 2 |
 ∴SA⊥AB,SA⊥AD;
∴SA⊥AB,SA⊥AD;∴SA⊥平面ABCD,CD?平面ABCD;
∴SA⊥CD,即CD⊥SA;
连接AC,∠ADC=60°,AD=CD;
∴△ACD为等边三角形,∴AE⊥CD,即CD⊥AE;
∴CD⊥平面SAE.
(2)取AB中点G,并过G作GF∥SA,交SB于F,连接CF;
∵CG∥AE,AE?平面SAE,CG?平面SAE;
∴CG∥平面SAE,同理可得FG∥平面SAE,FG∩CF=G;
∴平面CFG∥平面SAE,CF?平面CFG;
∴CF∥平面SAE,并且F为SB的中点.
这样就找到了点F.
点评:考查线面垂直的判定定理,线面平行的判定定理,面面平行的判定定理,面面平行的性质,注意要找一直线和一平面平行,转化为找直线所在平面和这个平面平行的办法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设变量x,y满足约束条件
,则目标函数z=x+y的最大值是( )
|
| A、3 | B、4 | C、5 | D、6 |
 如图所示,设F是抛物线E:x2=2py(p>0)的焦点,过点F作斜率分别为k1、k2的两条直线l1、l2,且k1•k2=-1,l1与E相交于点A、B,l2与E相交于点C,D.已知△AFO外接圆的圆心到抛物线的准线的距离为3(O为坐标原点).
如图所示,设F是抛物线E:x2=2py(p>0)的焦点,过点F作斜率分别为k1、k2的两条直线l1、l2,且k1•k2=-1,l1与E相交于点A、B,l2与E相交于点C,D.已知△AFO外接圆的圆心到抛物线的准线的距离为3(O为坐标原点).