题目内容
11.已知△ABC的面积为1,∠A的平分线交对边BC于D,AB=2AC,且AD=kAC,k∈R,则当k=$\frac{2\sqrt{10}}{5}$时,边BC的长度最短.分析 由题意,$\frac{1}{2}•2a•a•sinA$=1,sinA=$\frac{1}{{a}^{2}}$,求BC最短时k的值,考虑A为锐角或直角时即可,求出BC,利用导数知识,即可求解.
解答 解:由题意,$\frac{1}{2}•2a•a•sinA$=1,∴sinA=$\frac{1}{{a}^{2}}$,
求BC最短时k的值,考虑A为锐角或直角时即可,∴cosA=$\frac{\sqrt{{a}^{2}-1}}{{a}^{2}}$,
∴由余弦定理可得BC2=5a2-4$\sqrt{{a}^{4}-1}$,
设a2=t>0,则f(t)=5t-4$\sqrt{{t}^{2}-1}$,
f′(t)=5-$\frac{4t}{\sqrt{{t}^{2}-1}}$,
t>$\frac{5}{3}$,f′(t)>0,函数单调递增,0<t<$\frac{5}{3}$,f′(t)<0,函数单调递减,
∴t=$\frac{5}{3}$时,函数f(t)取得最小值,即BC=$\sqrt{3}$,
∴cosA=$\frac{4}{5}$=2cos2∠CAD-1,∴cos∠CAD=$\frac{3\sqrt{10}}{10}$,
∴k=$\frac{4}{3}$cos∠CAD=$\frac{2\sqrt{10}}{5}$.
故答案为:$\frac{2\sqrt{10}}{5}$.
点评 本题考查余弦定理的运用,考查导数知识,考查学生分析解决问题的能力,难度大.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案
相关题目
1.若变量x,y满足约束条件$\left\{\begin{array}{l}x+2y≤2\\ x+y≥0\\ x≤4\end{array}\right.$,则z=2x+y的最大值为( )
| A. | 2 | B. | 8 | C. | 5 | D. | 7 |
2.如图是某四棱锥的三视图,则该几何体的表面积等于( )
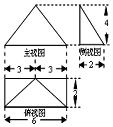

| A. | 34+6$\sqrt{5}$ | B. | 44+12$\sqrt{5}$ | C. | 34+6$\sqrt{3}$ | D. | 32+6$\sqrt{5}$ |
6.设函数f(x)=$\frac{1}{3}$x-lnx(x>0),则函数f(x)( )
| A. | 在区间(0,1)内有零点,在区间(1,+∞)内无零点 | |
| B. | 在区间(0,1)内有零点,在区间(1,+∞)内有零点 | |
| C. | 在区间(0,3),(3,+∞)均无零点 | |
| D. | 在区间(0,3),(3,+∞)均有零点 |
16.设全集U=R,A={x|-2<x<1},B={x|2x>1},则A∩(∁UB)=( )
| A. | (0,1) | B. | (-2,0) | C. | (-2,0] | D. | (-2,+∞) |
20.如图,在三棱柱ABC-A1B1C1中,M为A1C1的中点,若$\overrightarrow{AB}=\vec a$,$\overrightarrow{BC}=\vec b$,$\overrightarrow{A{A_1}}=\vec c$,则$\overrightarrow{BM}$可表示为( )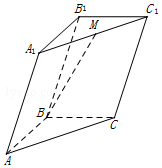

| A. | $-\frac{1}{2}\vec a+\frac{1}{2}\vec b+\vec c$ | B. | $\frac{1}{2}\vec a+\frac{1}{2}\vec b+\vec c$ | C. | $-\frac{1}{2}\vec a-\frac{1}{2}\vec b+\vec c$ | D. | $\frac{1}{2}\vec a-\frac{1}{2}\vec b+\vec c$ |