题目内容
8.分别用文字语言、图形语言和符号语言书写面面平行的判定定理.分析 面面平行判定定理的内容用文字叙述、图形语言以及几何符号表示,分别写出即可.
解答 解:面面平行的判定定理;
(1)文字语言是“如果两个一个平面内有两个相交直线与另一个平面平行,则这两个平面平行”;
(2)图形语言表示:如图所示:
(3)用符号语言表示:$\left\{\begin{array}{l}{a?α,b?α}\\{a∩b=P}\\{a∥β,b∥β}\end{array}\right.$⇒α∥β.
点评 本题考查了平面与平面平行的判定定理,熟练掌握平面平行的判定定理是解答本题的关键,是基础题.

练习册系列答案
相关题目
20.已知sin2θ=$\frac{3}{5}$,且0<2θ<$\frac{π}{2}$,则$\frac{2co{s}^{2}\frac{θ}{2}-sinθ-1}{\sqrt{2}sin(θ+\frac{π}{4})}$的值为( )
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | 3 |
16.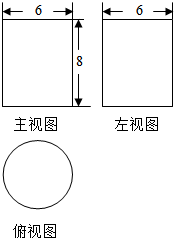 几何体的三视图如图所示,若从该几何体的实心外接球中挖去该几何体,则剩余几何体的表面积是(注:包括外表面积和内表面积)( )
几何体的三视图如图所示,若从该几何体的实心外接球中挖去该几何体,则剩余几何体的表面积是(注:包括外表面积和内表面积)( )
 几何体的三视图如图所示,若从该几何体的实心外接球中挖去该几何体,则剩余几何体的表面积是(注:包括外表面积和内表面积)( )
几何体的三视图如图所示,若从该几何体的实心外接球中挖去该几何体,则剩余几何体的表面积是(注:包括外表面积和内表面积)( )| A. | 133π | B. | 100π | C. | 66π | D. | 166π |
3.已知命题p:关于x的函数y=x2-3ax+4在[1,+∞)上是增函数,命题q:关于x的函数y=(2a-1)x在[1,+∞)上是减函数.若“p且q”为真命题,则实数a的取值范围是( )
| A. | (-∞,$\frac{2}{3}$] | B. | (0,$\frac{1}{2}$) | C. | ($\frac{1}{2}$,$\frac{2}{3}$] | D. | ($\frac{1}{2}$,1) |
17.通过随机询问某校高二年级学生在购买食物时是否看营养说明,得到如下列联表:
参考数据:
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(b+d)(a+c)(c+d)}$,n=a+b+c+d
(1)写出x,y,z的值
(2)根据以上列联表,问有多大把握认为“性别在购买食物时看营养说明”有关?
(3)从女生中按是否看营养说明采取分层抽样,抽取容量为5的样本,再从这5名女生中随机选取两名作深度访谈.求选到看与不看营养说明的女生各一名的概率.
| 男生 | 女生 | 总计 | |
| 看营养说明 | 50 | 30 | 80 |
| 不看营养说明 | 10 | x | y |
| 总计 | 60 | z | 110 |
| P(K2≥K) | 0.10 | 0.05 | 0.01 | 0.005 |
| K | 2.706 | 3.841 | 6.635 | 7.879 |
(1)写出x,y,z的值
(2)根据以上列联表,问有多大把握认为“性别在购买食物时看营养说明”有关?
(3)从女生中按是否看营养说明采取分层抽样,抽取容量为5的样本,再从这5名女生中随机选取两名作深度访谈.求选到看与不看营养说明的女生各一名的概率.
 如图,F1,F2是椭圆${C_1}:\frac{x^2}{12}+\frac{y^2}{4}=1$与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是$\sqrt{2}$.
如图,F1,F2是椭圆${C_1}:\frac{x^2}{12}+\frac{y^2}{4}=1$与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是$\sqrt{2}$.