题目内容
19.画出下列函数的图象,(用虚线保留作图痕迹),并根据图象写出函数的单调区间:
(1)f(x)=log2(x+1)
(2)f(x)=x2-2|x|-3.
分析 (1)作函数y=log2x的图象,向左平移1个单位即可,从而写出单调区间;
(2)作函数f(x)=x2-2|x|-3的图象,从而写出单调区间.
解答 解:(1)作函数y=log2x的图象,向左平移1个单位即可,如下图; ,
,
f(x)=log2(x+1)的单调递增区间 (-1,+∞);
(2)作函数f(x)=x2-2|x|-3的图象如下,
故函数的单调递增区间 (-1,0)和(1,+∞),单调递减区间 (-∞,-1)和(0,1).
点评 本题考查了学生的作图能力及数形结合的思想应用,同时考查了图象的变换.

练习册系列答案
相关题目
6.某年青教师近五年内所带班级的数学平均成绩统计数据如表:
(1)利用所给数据,求出平均分与年份之间的回归直线方程$\hat y=bx+a$
(2)利用(1)中所求出的直线方程预测该教师2015年所带班级的数学平均成绩.
参考公式:b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-$\widehat{b}$$\overline{x}$.
| 年份x年 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 平均成绩y分 | 97 | 98 | 103 | 108 | 109 |
(2)利用(1)中所求出的直线方程预测该教师2015年所带班级的数学平均成绩.
参考公式:b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-$\widehat{b}$$\overline{x}$.
 甲、乙两人在5次综合测评中成绩的茎叶图如图所示,其中一个数字被污染,记甲、乙的平均成绩为$\overrightarrow{{x}_{甲}}$,$\overrightarrow{{x}_{乙}}$,则$\overrightarrow{{x}_{甲}}$>$\overrightarrow{{x}_{乙}}$的概率是$\frac{2}{5}$.
甲、乙两人在5次综合测评中成绩的茎叶图如图所示,其中一个数字被污染,记甲、乙的平均成绩为$\overrightarrow{{x}_{甲}}$,$\overrightarrow{{x}_{乙}}$,则$\overrightarrow{{x}_{甲}}$>$\overrightarrow{{x}_{乙}}$的概率是$\frac{2}{5}$.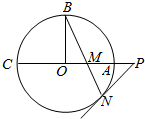 如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于N,过N 点的切线交C A 的延长线于P
如图,圆O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交圆O于N,过N 点的切线交C A 的延长线于P