题目内容
2.已知函数f(x)=|a-x|(a∈R)(Ⅰ)当a=$\frac{3}{2}$时,求使不等式f(2x-$\frac{3}{2}$)>2f(x+2)+2成立的x的集合A;
(Ⅱ)设x0∈A,证明f(x0x)≥x0f(x)+f(ax0).
分析 (Ⅰ)把a的值代入不等式化简后,对x分类讨论,分别去掉绝对值求出每个不等式的解集,再取并集即得不等式的解集;
(Ⅱ)由(I)和x0∈A求出x0的范围,化简f(x0x)-x0f(x)后利用绝对值三角不等式证明结论成立.
解答 解:(Ⅰ)当a=$\frac{3}{2}$时,原不等式化为:|x-$\frac{3}{2}$|-|x+$\frac{1}{2}$|>1①,-----1分
当x$≤-\frac{1}{2}$时,①式化为:$\frac{3}{2}$-x+x+$\frac{1}{2}$>1恒成立,
即x$≤-\frac{1}{2}$;-----2分
当$-\frac{1}{2}$<x<$\frac{3}{2}$时,①式化为:$\frac{3}{2}$-x-x-$\frac{1}{2}$>1恒成立,
解得x<0,即$-\frac{1}{2}$<x<0;------3分
当x≥$\frac{3}{2}$时,①式化为:-$\frac{3}{2}$+x-x-$\frac{1}{2}$>1无解,-------4分
综上,原不等式的解集A=(-∞,0);------5分
证明:(Ⅱ)因为x0∈A,所以x0<0,
又f(x)=|a-x|,-------6分
所以f(x0x)-x0f(x)=|a-x0x|-x0|a-x|
=|a-x0x|+|-x0a+x0x|≥|a-x0x-x0a+x0x|
=|a-ax0|=f(ax0),-------9分
所以f(x0x)≥x0f(x)+f(ax0).-------10分
点评 本题考查绝对值不等式的解法,以及绝对值三角不等式的应用,体现了等价转化以及分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
10.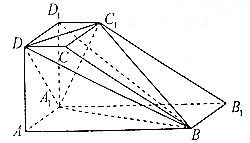 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.
(Ⅰ)证明:BD1⊥平面A1C1D;
(Ⅱ)求多面体BDC1A1D1的体积.
 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.(Ⅰ)证明:BD1⊥平面A1C1D;
(Ⅱ)求多面体BDC1A1D1的体积.
14.设F1,F2是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的两个焦点,若点P在双曲线上,且∠F1PF2=90°,|PF1|•|PF2|=2,则b=( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
11.已知F1、F2为双曲线的焦点,过F2垂直于实轴的直线交双曲线于A、B两点,BF1交y轴于点C,若AC⊥BF1,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
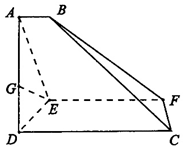 如图,已知梯形CDEF与△ADE所在的平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9,CD=12,连接BC,BF.
如图,已知梯形CDEF与△ADE所在的平面垂直,AD⊥DE,CD⊥DE,AB∥CD∥EF,AE=2DE=8,AB=3,EF=9,CD=12,连接BC,BF.