题目内容
已知f(x)=asinωx+bcosωx(ω>0,x∈R)的相邻两个对称轴之间的距离为
,且满足f(x)≥f(
)=-1.
(1)求f(x)的解析式;
(2)试列表并用“五点法”画出函数y=f(x)在区间[-
,
]上的图象.
(3)若函数g(x)=f(
-x),求函数y=g(x)的单调递减区间.
| π |
| 2 |
| 2π |
| 3 |
(1)求f(x)的解析式;
(2)试列表并用“五点法”画出函数y=f(x)在区间[-
| π |
| 12 |
| 11π |
| 12 |
(3)若函数g(x)=f(
| π |
| 2 |
考点:五点法作函数y=Asin(ωx+φ)的图象,三角函数中的恒等变换应用,正弦函数的图象
专题:三角函数的图像与性质
分析:(1)根据函数的性质求出a,b即可求f(x)的解析式;
(2)利用“五点法”即可画出函数y=f(x)在区间[-
,
]上的图象.
(3)求出函数g(x)=f(
-x)的表达式,根据三角函数的单调性即可求函数y=g(x)的单调递减区间.
(2)利用“五点法”即可画出函数y=f(x)在区间[-
| π |
| 12 |
| 11π |
| 12 |
(3)求出函数g(x)=f(
| π |
| 2 |
解答:
解:(1)f(x)=asinωx+bcosωx=
sin(ωx+φ),其中tanφ=
,
则函数的周期T=
,
∵函数f(x)相邻两个对称轴之间的距离为
,
∴函数的周期T=2×
=
,
解得ω=2,
即f(x)=asin2x+bcos2x,
∵f(x)≥f(
)=-1,
∴函数的最小值为-1,即
asin(2×
)+bcos(2×
)=-1,
即
a+
=1①
且-
=-1,即a2+b2=1 ②,
解得a=
,b=
f(x)=
sin2x+
cos2x=sin(2x+
);
(2)列表并用“五点法”画出函数y=f(x)在区间[-
,
]上的图象.
画图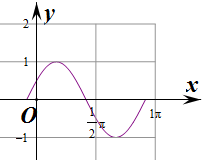
(3)函数g(x)=f(
-x)=sin[2(
-x)+
]=sin(
-2x)=-sin(
-2x)=sin(2x-
);
由2kπ+
≤2x-
≤2kπ+
,k∈Z,
解得kπ+
≤x≤kπ+
,k∈Z
即函数y=g(x)的单调递减区间是[kπ+
,kπ+
],k∈Z.
| a2+b2 |
| b |
| a |
则函数的周期T=
| 2π |
| ω |
∵函数f(x)相邻两个对称轴之间的距离为
| π |
| 2 |
∴函数的周期T=2×
| π |
| 2 |
| 2π |
| ω |
解得ω=2,
即f(x)=asin2x+bcos2x,
∵f(x)≥f(
| 2π |
| 3 |
∴函数的最小值为-1,即
asin(2×
| 2π |
| 3 |
| 2π |
| 3 |
即
| ||
| 2 |
| b |
| 2 |
且-
| a2+b2 |
解得a=
| ||
| 2 |
| 1 |
| 2 |
f(x)=
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
(2)列表并用“五点法”画出函数y=f(x)在区间[-
| π |
| 12 |
| 11π |
| 12 |
2x+
| 0 |
| π |
| 2π | ||||||||||
| x | -
|
|
|
|
| ||||||||||
y=sin(2x+
| 0 | 1 | 0 | -1 | 0 |

(3)函数g(x)=f(
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| 7π |
| 6 |
| π |
| 6 |
| π |
| 6 |
由2kπ+
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
解得kπ+
| π |
| 3 |
| 5π |
| 12 |
即函数y=g(x)的单调递减区间是[kπ+
| π |
| 3 |
| 5π |
| 12 |
点评:本题主要考查三角函数的图象和性质,利用条件求出函数的解析式是解决本题的关键.

练习册系列答案
相关题目
方程(x-y-3)(x+y)=0所表示的图形是( )
| A、两条互相平行的直线 | ||||
| B、两条互相垂直的直线 | ||||
C、一个点(
| ||||
D、过点(
|
已知实数x,y满足
,若z=kx-y的最大值为1,则实数k的取值范围是( )
|
| A、k=1 | B、k≤1 |
| C、k≥1 | D、0≤k≤1 |
一个人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是( )
| A、至多有一次中靶 |
| B、两次都中靶 |
| C、只有一次中靶 |
| D、两次都不中靶 |
已知x+x-1=3,那么与x2-x-2的值为( )
A、3
| ||
B、-
| ||
C、±3
| ||
D、±
|
 某品牌空调在元旦期间举行促销活动,所示的茎叶图表示某专卖店记录的每天销售量情况(单位:台),则销售量的中位数是( )
某品牌空调在元旦期间举行促销活动,所示的茎叶图表示某专卖店记录的每天销售量情况(单位:台),则销售量的中位数是( )| A、13 | B、14 | C、15 | D、16 |
已知等比数列{an}的公比为正数,且a1•a7=2a32,若a2=2,则a1=( )
| A、1 | ||
| B、4 | ||
C、
| ||
D、2
|