题目内容
15.小明每天早上在6:30~7:30之间离开家去上学,小强每天早上6:00~7:00之间到达小明家,约小明一同前往学校,则小强能见到小明的概率是( )| A. | 1 | B. | $\frac{3}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{1}{8}$ |
分析 设小明离开家去上学的时间为x,小强到达小明家的时间为y,建立平面直角坐标系,则(x,y)可以看成平面中的点,分析可得由试验的全部结果所构成的区域并求出其面积,同理可得小强能见到小明(事件A)事件所构成的区域及其面积,由几何概型公式,计算可得答案.
解答 解:设小明离开家去上学的时间为x,小强到达小明家的时间为y,
可得由试验的全部结果满足条件为$\left\{\begin{array}{l}{6.5≤x≤7.5}\\{6≤y≤7}\end{array}\right.$,所构成的区域的面积为s=1×1=1.
可得小强能见到小明(事件A)事件满足条件$\left\{\begin{array}{l}{6.5≤x≤7.5}\\{6≤y≤7}\\{x≤y}\end{array}\right.$,所构成的区域的面积为s′=1-$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}=\frac{7}{8}$.
故选:C.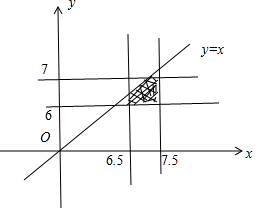
点评 本题考查几何概型的会面问题,准确作图利用面积作为几何测度是解决问题的关键,属中档题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
10.能反映样本数据的离散程度大小的数字特征是( )
| A. | 众数 | B. | 平均数 | C. | 中位数 | D. | 标准差 |
20.某高校从4名男大学生志愿者和3名女大学生志愿者中选3名派到3所学校支教(每所学校1名志愿者),要求这3名志愿者中男、女大学生都有,则不同的选派方案共有( )
| A. | 210种 | B. | 180种 | C. | 150种 | D. | 120种 |
20.下列说法正确的是( )
| A. | 命题“若x2=1,则x=1”是真命题 | |
| B. | 命题“若x2-5x+6=0,则x=2”的逆命题是“若x≠2,则x2-5x+6≠0” | |
| C. | 命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题 | |
| D. | 命题“若x=2,则x2-5x+6=0”的否命题是“若x=2,则x2-5x+6≠0” |
 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,△PAB为等边三角形,O为AB的中点,PO丄AC.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,△PAB为等边三角形,O为AB的中点,PO丄AC. 如图,菱形ABCD中,∠A=60°,沿BD折成直二面角A-BD-C,过点A作PA⊥平面ABD,连接AC、PC、PD.
如图,菱形ABCD中,∠A=60°,沿BD折成直二面角A-BD-C,过点A作PA⊥平面ABD,连接AC、PC、PD.