题目内容
设点O为坐标原点，A（2，1），且点F（x，y）坐标满足
，则|
|•cos∠AOP的最大值为 ．
|
| OP |
考点：简单线性规划
专题：不等式的解法及应用
分析：先画出满足
的可行域，再根据平面向量的运算性质，对|
|•cos∠AOP进行化简，结合可行域，即可得到最终的结果．
|
| OP |
解答：
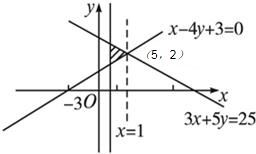解：满足
的可行域如图所示，
又∵|
|•cos∠AOP=
，
∵
=（2，1），
=（x，y），
∴|
|•cos∠AOP=
．
由图可知，平面区域内x值最大的点为（5，2）
|
|•cos∠AOP的最大值为：
故答案为：
．
解：满足
|
又∵|
| OP |
| ||||
|
|
∵
| OA |
| OP |
∴|
| OP |
| 2x+y | ||
|
由图可知，平面区域内x值最大的点为（5，2）
|
| OP |
12
| ||
| 5 |
故答案为：
12
| ||
| 5 |
点评：用图解法解决线性规划问题时，分析题目的已知条件，找出约束条件和目标函数是关键，可先将题目中的量分类、列出表格，理清头绪，然后列出不等式组（方程组）寻求约束条件，并就题目所述找出目标函数．然后将可行域各角点的值一一代入，最后比较，即可得到目标函数的最优解．
练习册系列答案
阅读快车系列答案
相关题目
在△ABC中，D在BC上，
=2
，设
=
，
=
，则
=（ ）
| BD |
| DC |
| AB |
| a |
| AC |
| b |
| AD |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
下列说法正确的是（ ）
| A、命题q：?x∈R，x2+x+1＜0是真命题 |
| B、“x=1”是“x2-3x+2=0”的充分必要条件 |
| C、若p且q为假命题，则p和q均为假命题 |
| D、“若x2-3x+2=0，则x=1”的逆否命题为：“若x≠1则x2-3x+2≠0” |