题目内容
已知变量x,y满足约束条件
,则z=22x+y的最大值为 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:由约束条件画出可行域,令t=2x+y,化为直线方程的斜截式,数形结合得到最优解,联立方程组求出最优解的坐标,求出t的最大值,代入z=22x+y得答案.
解答:
解:由约束条件
作差可行域如图,
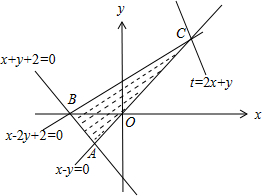
联立
,解得C(2,2),
令t=2x+y,得:y=-2x+t,由图可知,
当直线y=-2x+t过C(2,2)时,t最大,为2×2+2=6.
此时z=22x+y的最大值为26=64.
故答案为:64.
|

联立
|
令t=2x+y,得:y=-2x+t,由图可知,
当直线y=-2x+t过C(2,2)时,t最大,为2×2+2=6.
此时z=22x+y的最大值为26=64.
故答案为:64.
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,考查了指数函数的单调性,是中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
 a为如图所示的程序框图中输出的结果,则化简cos(aπ-θ)的结果是( )
a为如图所示的程序框图中输出的结果,则化简cos(aπ-θ)的结果是( )| A、cosθ | B、-cosθ |
| C、sinθ | D、-sinθ |
二项式(x2-
)5的展开式中x4的项的系数为( )
| 1 |
| x |
| A、15 | B、-15 |
| C、10 | D、-10 |