题目内容
14.已知数列{an}满足a1=3,且对任意的正整数m,n都有an+m=an•am,若数列{bn}满足bn=n-1+log3an,{bn}的前n项和为Bn.(Ⅰ)求an和Bn;
(Ⅱ)令cn=an•bn,dn=$\frac{4n+4}{{B}_{n}•{B}_{n+2}}$,数列{cn}的前n项和为Sn,数列{dn}的前n项和为Tn,分别求Sn和Tn.
分析 (I)对任意的正整数m,n都有an+m=an•am,可得an+1=an•a1=3an,利用等比数列的通项公式可得an.可得bn,即可得出{bn}的前n项和为Bn.
(II)cn=(2n-1)•3n.利用“错位相减法”与等比数列的前n项和公式可得Sn.dn=$\frac{4n+4}{{B}_{n}•{B}_{n+2}}$=$\frac{4n+4}{{n}^{2}(n+2)^{2}}$=$\frac{1}{{n}^{2}}-\frac{1}{(n+2)^{2}}$,利用“裂项求和”即可得出.
解答 解:(I)∵对任意的正整数m,n都有an+m=an•am,
∴an+1=an•a1=3an,
∴数列{an}是等比数列,公比为3,首项为3,∴an=3n.
∴bn=n-1+log3an=n-1+n=2n-1,
∴{bn}的前n项和为Bn=$\frac{n(1+2n-1)}{2}$=n2.
(II)cn=an•bn,=(2n-1)•3n.
∴数列{cn}的前n项和为Sn=3+3×32+5×33+…+(2n-1)•3n,
∴3Sn=32+3×33+…+(2n-3)•3n+(2n-1)•3n+1,
∴-2Sn=3+2(32+33+…+3n)-(2n-1)•3n+1=$\frac{2×3({3}^{n}-1)}{3-1}$-3-(2n-1)•3n+1=(2-2n)•3n+1-6,
∴Sn=(n-1)•3n+1+3.
dn=$\frac{4n+4}{{B}_{n}•{B}_{n+2}}$=$\frac{4n+4}{{n}^{2}(n+2)^{2}}$=$\frac{1}{{n}^{2}}-\frac{1}{(n+2)^{2}}$,
当n=1时,d1=$\frac{8}{9}$;
当n≥2时,Tn=$(1-\frac{1}{{3}^{2}})$+$(\frac{1}{{2}^{2}}-\frac{1}{{4}^{2}})$+$(\frac{1}{{3}^{2}}-\frac{1}{{5}^{2}})$+…+$(\frac{1}{(n-1)^{2}}-\frac{1}{(n+1)^{2}})$+$(\frac{1}{{n}^{2}}-\frac{1}{(n+2)^{2}})$=$\frac{5}{4}$-$\frac{1}{(n+1)^{2}}$-$\frac{1}{(n+2)^{2}}$.
当n=1时也成立,∴Tn=$\frac{5}{4}$-$\frac{1}{(n+1)^{2}}$-$\frac{1}{(n+2)^{2}}$.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、“裂项求和”方法、“错位相减法”,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
| A. | (-1,-$\frac{1}{3}$) | B. | (-∞,-1) | C. | (-$\frac{1}{3}$,+∞) | D. | (-∞,-1)∪(-$\frac{1}{3}$,+∞) |
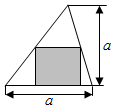 在底和高等长度的锐角三角形中有一个内接矩形,矩形的一边在三角形的底边上,如图,在三角形内取一点,则该点落入矩形内的最大概率为( )
在底和高等长度的锐角三角形中有一个内接矩形,矩形的一边在三角形的底边上,如图,在三角形内取一点,则该点落入矩形内的最大概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |