题目内容
8.已知函数f(x)=|x-2|.(1)解不等f(x)+f(x+1)≥5;
(2)若|a|>1且f(ab)>|a|•f(${\frac{b}{a}}$),证明:|b|>2.
分析 (1)通过讨论x的范围,去掉绝对值号,解不等式即可;(2)求出f(ab)和f($\frac{b}{a}$),代入不等式,问题转化为|ab-2|>|b-2a|,平方证明即可.
解答 (1)解:原不等式等价于|x-2|+|x-1|≥5,
当x>2时,不等式可化为:(x-2)+(x-1)≥5,
解得:x≥4,
当1≤x≤2时,不等式可化为(2-x)+(x-1)≥5,1≥5,无解,
x<1时,不等式可化为:(2-x)+(1-x)≥5,解得:x≤-1,
综上,不等式的解集是{x|x≥4或x≤-1};
(2)证明:$f({ab})>|a|•f({\frac{b}{a}})$
?|ab-2|>|a||$\frac{b}{a}$-2|
?|ab-2|>|b-2a|
?(ab-2)2>(b-2a)2
?a2b2+4-b2-4a2>0
?(a2-1)(b2-4)>0,
∵|a|>1,
∴a2-1>0,
∴b2-4>0,
∴|b|>2,证毕.
点评 本题考查了解绝对值不等式问题,考查不等式的证明,是一道中档题.

练习册系列答案
相关题目
18.如图,在梯形ABCD中,AB=3CD,则下列判断正确的是( )
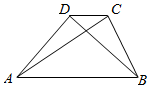

| A. | $\overrightarrow{AB}$=3$\overrightarrow{CD}$ | B. | $\overrightarrow{AC}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\overrightarrow{AD}$ | C. | $\overrightarrow{BD}$=$\overrightarrow{AB}$-$\overrightarrow{AD}$ | D. | $\overrightarrow{BC}$=-$\frac{2}{3}$$\overrightarrow{AB}$+$\overrightarrow{AD}$ |
19.已知函数f(x)=x2(ex+e-x)-(2x+1)2(e2x+1+e-2x-1),则满足f(x)>0的实数x的取值范围为( )
| A. | (-1,-$\frac{1}{3}$) | B. | (-∞,-1) | C. | (-$\frac{1}{3}$,+∞) | D. | (-∞,-1)∪(-$\frac{1}{3}$,+∞) |
16.定义在R上的函数f(x)满足f(x+1)=2f(x),且当0≤x≤1时,f(x)=x2-x,则$f({-\frac{3}{2}})$=( )
| A. | $-\frac{1}{2}$ | B. | $-\frac{1}{4}$ | C. | $-\frac{1}{8}$ | D. | $-\frac{1}{16}$ |
3.T为常数,定义fT(x)=$\left\{\begin{array}{l}f(x),f(x)≥T\\ T,f(x)<T\end{array}\right.$,若f(x)=x-lnx,则f3[f2(e)]的值为.( )
| A. | e-l | B. | e | C. | 3 | D. | e+l |
17.已知集合A={x|-3<x<2},B={x|3x>1},则A∩(∁RB)=( )
| A. | (-3,1] | B. | (1,2) | C. | (-3,0] | D. | [1,2) |
 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<φ<$\frac{π}{2}$)的图象如图所示.
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<φ<$\frac{π}{2}$)的图象如图所示.