题目内容
15.已知函数y=f(x)的图象是自原点出发的一条折线,当n≤y≤n+1(n=0,1,2,…)时,该图象是斜率为bn的线段,其中常数b>0且b≠1,数列{xn}由f(xn)=n(n=0,1,2…)定义.(1)若b=3,求x1,x2;
(2)求xn的表达式及f(x)的解析式(不必求f(x)的定义域);
(3)当b>1时,求f(x)的定义域,并证明y=f(x)的图象与y=x的图象没有横坐标大于1的公共点.
分析 (1)由f(0)=0,运用直线的斜率公式,f(xn)=n,可得x1,x2;
(2)由x1=1,x2=1+$\frac{1}{b}$,…,xn=x1+(x2-x1)+(x3-x2)+…+(xn-xn-1),运用等比数列的求和公式,即可得到所求;再由直线的斜率公式可得f(x)的解析式;
(3)当b>1时,$\underset{lim}{x→∞}$xn=$\frac{b}{b-1}$,f(x)的定义域为[0,$\frac{b}{b-1}$),证明b>1,1<x<$\frac{b}{b-1}$时,恒有f(x)>x成立.运用f(x)的解析式,结合不等式的性质即可得到结论.
解答 解:(1)依题意f(0)=0,又由f(x1)=1,当0≤y≤1时,
函数y=f(x)的图象是斜率为b0=1的线段,
故由$\frac{f({x}_{1})-f(0)}{{x}_{1}-0}$=1,得x1=1.
又由f(x2)=2,当1≤y≤2时,函数y=f(x)的图象是斜率为b的线段,
故由$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$=b,
即x2-x1=$\frac{1}{b}$=$\frac{1}{3}$,解得x2=$\frac{4}{3}$;
(2)由(1)可得x1=1,x2=1+$\frac{1}{b}$,
由函数y=f(x)图象中第n段线段的斜率为bn-1,
故得$\frac{f({x}_{n})-f({x}_{n-1})}{{x}_{n}-{x}_{n-1}}$=bn-1,
又f(xn)=n,f(xn-1)=n-1,
∴xn-xn-1=($\frac{1}{b}$)n-1,
由此知数列{xn-xn-1}为等比数列,其首项为1,公比为$\frac{1}{b}$,
因b≠1,得xn=x1+(x2-x1)+(x3-x2)+…+(xn-xn-1)
=1+$\frac{1}{b}$+($\frac{1}{b}$)2+…+=($\frac{1}{b}$)n-1=$\frac{b-(\frac{1}{b})^{n-1}}{b-1}$=$\frac{{b}^{n}-1}{{b}^{n}-{b}^{n-1}}$,
对n=1也成立,故xn=$\frac{{b}^{n}-1}{{b}^{n}-{b}^{n-1}}$;
当n≤y≤n+1时,$\frac{f(x)-f({x}_{n})}{x-{x}_{n}}$=bn,
f(x)=f(xn)+(x-xn)bn=n+(x-xn)bn(n=0,1,2,…):
(3)当b>1时,$\underset{lim}{x→∞}$xn=$\frac{b}{b-1}$,f(x)的定义域为[0,$\frac{b}{b-1}$),
下面证明b>1,1<x<$\frac{b}{b-1}$时,恒有f(x)>x成立.
事实上,对1<x<$\frac{b}{b-1}$时,存在xn,使xn≤x≤xn+1,
于是由b>1时,f(x)=f(xn)=bn(x-xn)>x-xn,
进而f(x)-x>f(xn)-xn=n-xn,
当b>1时,xn=1+$\frac{1}{b}$+$\frac{1}{{b}^{2}}$+…+$\frac{1}{{b}^{n-1}}$<n,
即n-xn>0,可得f(x)>x.
综上知,y=f(x)的图象与y=x的图象没有横坐标大于1的公共点
点评 本题主要考查函数的基本概念、等比数列、数列极限的基础知识,考查归纳、推理和综合的能力,属于中档题.

 一线名师权威作业本系列答案
一线名师权威作业本系列答案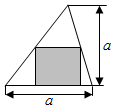 在底和高等长度的锐角三角形中有一个内接矩形,矩形的一边在三角形的底边上,如图,在三角形内取一点,则该点落入矩形内的最大概率为( )
在底和高等长度的锐角三角形中有一个内接矩形,矩形的一边在三角形的底边上,如图,在三角形内取一点,则该点落入矩形内的最大概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)是偶函数,它的部分图象如图所示.M是函数f(x)图象上的点,K,L是函数f(x)的图象与x轴的交点,且△KLM为等腰直角三角形,则f(x)=$\frac{1}{2}$cosπx.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)是偶函数,它的部分图象如图所示.M是函数f(x)图象上的点,K,L是函数f(x)的图象与x轴的交点,且△KLM为等腰直角三角形,则f(x)=$\frac{1}{2}$cosπx.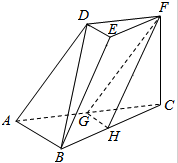 如图,三棱台DEF-ABC中,底面是以AB为斜边的直角三角形,FC⊥底面ABC,AB=2DE,G,H分别为AC,BC的中点.
如图,三棱台DEF-ABC中,底面是以AB为斜边的直角三角形,FC⊥底面ABC,AB=2DE,G,H分别为AC,BC的中点.