题目内容
已知向量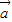 =(2,0),
=(2,0),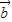 =(1,4).
=(1,4).(Ⅰ)求|
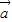 +
+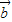 |的值;
|的值;(Ⅱ)若向量k
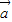
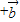 与
与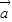 +2
+2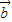 平行,求k的值;
平行,求k的值;(Ⅲ)若向量k
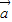 +
+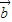 与
与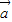 +2
+2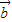 的夹角为锐角,求k的取值范围.
的夹角为锐角,求k的取值范围.
【答案】分析:(Ⅰ)先求向量的坐标,即可求|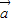 +
+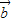 |的值;
|的值;
(Ⅱ)确定向量k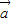
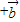 ,
,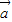 +2
+2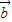 的坐标,利用平行的条件,即可求k的值;
的坐标,利用平行的条件,即可求k的值;
(Ⅲ)向量k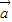 +
+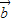 与
与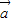 +2
+2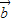 的夹角为锐角,则数量积大于0且不共线,即可求k的取值范围.
的夹角为锐角,则数量积大于0且不共线,即可求k的取值范围.
解答:解:(Ⅰ)依题意得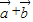 =(3,4),∴|
=(3,4),∴|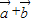 |=
|=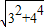 =5
=5
(Ⅱ)依题意得k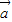
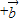 =(2k+1,4),
=(2k+1,4),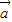 +2
+2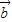 =(4,8)
=(4,8)
∵向量k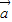
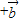 与
与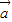 +2
+2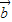 平行
平行
∴8×(2k+1)-4×4=0,解得k=
(Ⅲ)由(Ⅱ)得k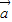
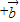 =(2k+1,4),
=(2k+1,4),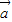 +2
+2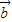 =(4,8)
=(4,8)
∵向量k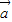 +
+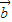 与
与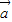 +2
+2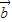 的夹角为锐角,
的夹角为锐角,
∴4×(2k+1)+4×8>0,且8×(2k+1)≠4×4
∴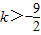 且k≠
且k≠ .
.
点评:本题考查向量知识的运用,考查向量模的计算,考查向量的共线,考查学生分析解决问题的能力,属于中档题.
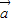 +
+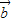 |的值;
|的值;(Ⅱ)确定向量k
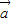
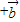 ,
,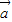 +2
+2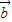 的坐标,利用平行的条件,即可求k的值;
的坐标,利用平行的条件,即可求k的值;(Ⅲ)向量k
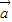 +
+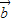 与
与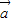 +2
+2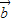 的夹角为锐角,则数量积大于0且不共线,即可求k的取值范围.
的夹角为锐角,则数量积大于0且不共线,即可求k的取值范围.解答:解:(Ⅰ)依题意得
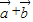 =(3,4),∴|
=(3,4),∴|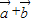 |=
|=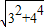 =5
=5(Ⅱ)依题意得k
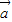
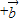 =(2k+1,4),
=(2k+1,4),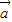 +2
+2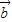 =(4,8)
=(4,8)∵向量k
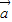
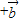 与
与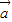 +2
+2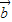 平行
平行∴8×(2k+1)-4×4=0,解得k=

(Ⅲ)由(Ⅱ)得k
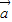
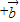 =(2k+1,4),
=(2k+1,4),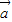 +2
+2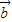 =(4,8)
=(4,8)∵向量k
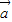 +
+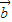 与
与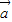 +2
+2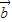 的夹角为锐角,
的夹角为锐角,∴4×(2k+1)+4×8>0,且8×(2k+1)≠4×4
∴
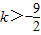 且k≠
且k≠ .
.点评:本题考查向量知识的运用,考查向量模的计算,考查向量的共线,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
已知向量
=(
,0),
=(
,
),
=(cosα,sinα)( α∈R),则
与
夹角的取值范围是( )
| OB |
| 2 |
| OC |
| 2 |
| 2 |
| CA |
| OA |
| OB |
A、[0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
已知向量
=(2,0),向量
=(2,2),向量
=(
cosα,
sinα),则向量
与向量
的夹角范围为( )
| OB |
| OC |
| CA |
| 2 |
| 2 |
| OA |
| OB |
A、[0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
已知向量
=(2,0),
=(2,2),
=(-1,-3),则
和
的夹角为( )
| OB |
| OC |
| CA |
| OA |
| OB |
A、
| ||
B、
| ||
C、
| ||
D、
|