题目内容

2．已知tanα=-3，借助三角函数定义求sinα和cosα．

分析 取点，求r，再利用三角函数的定义，即可得出结论．

解答 解：由题意，取点（-1，3），则r=$\sqrt{10}$，sinα=$\frac{3\sqrt{10}}{10}$，cosα=-$\frac{\sqrt{10}}{10}$；
取点（1，-3），则r=$\sqrt{10}$，sinα=-$\frac{3\sqrt{10}}{10}$，cosα=$\frac{\sqrt{10}}{10}$．

点评 本题考查三角函数的定义，考查学生的计算能力，比较基础．

练习册系列答案
相关题目
12．下列说法正确的是（　　）
A．命题“若x2=1，则x=1”的否命题为“若x2=1，则x≠1”
B．命题“?x≥0，x2+x-1＜0”的否定是“?x＜0，x2+x-1＜0”
C．“x=-1”是“x2-5x-6=0”的必要不充分条件
D．命题“若x=y，则sinx=siny”的逆否命题为真命题．
13．函数f（x）=sin（ωx+ϕ）$（ω＞0，0＜ϕ＜\frac{π}{2}）$，f（0）=$\frac{{\sqrt{2}}}{2}$，且对任意${x_1}，{x_2}∈（\frac{π}{2}，π）$均满足$\frac{{{x_1}-{x_2}}}{{f（{x_1}）-f（{x_2}）}}＜0（{x_1}≠{x_2}）$，则ω的取值范围是$\frac{1}{2}$≤ω≤$\frac{5}{4}$．
10．已知函数f（x）=|x-t|+$\frac{t}{x}$（x＞0）；
（1）判断函数y=f（x）在区间（0，t]上的单调性，并证明；
（2）若函数y=f（x）的最小值为与t无关的常数，求实数t的取值范围．
17．如图所示，在△ABC中，M在BC上，N在AM上，CM=CN，且$\frac{AM}{AN}$=$\frac{BM}{CN}$，下列结论中正确的是（　　）
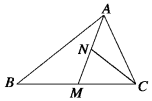
A．△ABM∽△ACBB．△ANC∽△AMBC．△ANC∽△ACMD．△CMN∽△BCA
7．已知函数$f（x）=\left\{{\begin{array}{l}{x+2}&{（{x≤-1}）}&{\;}\\{2x}&{（{-1＜x＜2}）}&{\;}\\{\frac{x^2}{2}}&{（{x≥2}）}&{\;}\end{array}}\right.$则$f[{f（{-\frac{7}{4}}）}]$=（　　）
A．$\frac{1}{4}$B．-7C．$\frac{1}{8}$D．$\frac{1}{2}$
14．已知二次函数f（x）满足f（0）=1且f（x+1）-f（x）=2x+2．
（Ⅰ）求f（x）的解析式； 
（Ⅱ）若g（x）=2f（x），x∈[-1，1]，求g（x）的值域．
11．如图，四棱锥P-ABCD中，所有棱长均为2，O是底面正方形ABCD中心，E为PC中点，则直线OE与直线PD所成角为（　　）
A．30°B．60°C．45°D．90°
1．已知函数$f（x）=\frac{1}{3}a{x^3}+\frac{1}{2}（a+1）{x^2}-（a+2）x+6$的极大值是f（-3）=15，
（1）是否存在极小值？若存在求出极小值．若不存在说明理由；
（2）求函数f（x）的单调区间．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网