题目内容
用0,1,2,3,5,这五个数组成没有重复数字的三位数,假设每个三位数的取法都是等可能的.
(Ⅰ)求三位数是偶数或能被5整除的数的概率;
(Ⅱ)若从这些三位偶数中任取二个数,用X表示能被3整除的三位偶数的个数,求X的分布列和数学期望.
(Ⅰ)求三位数是偶数或能被5整除的数的概率;
(Ⅱ)若从这些三位偶数中任取二个数,用X表示能被3整除的三位偶数的个数,求X的分布列和数学期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式,离散型随机变量及其分布列
专题:计算题,概率与统计
分析:(Ⅰ)五个数组成没有重复数字的三位数,共有
-
=48个数;分别计算个位数是0,2,5的三位数的个数,从而求概率;
(Ⅱ)由(Ⅰ)知,三位偶数共有21个,再找到能被3整除的数的个数,从而列分布列并求数学期望.
| A | 3 5 |
| A | 2 4 |
(Ⅱ)由(Ⅰ)知,三位偶数共有21个,再找到能被3整除的数的个数,从而列分布列并求数学期望.
解答:
解:(Ⅰ)五个数组成没有重复数字的三位数,共有
-
=48个数;
个位数是0,
=12个,
个位数是2,
-
=9个,
个位数是5,
-
=9个,
故三位数是偶数或能被5整除的数的概率为
=
;
(Ⅱ)由(Ⅰ)知,三位偶数共有21个,
个位数是0且能被3整除的数其十位数字与百位数字有(1,2),(1,5)排序,故共有4个;
个位数是2且能被3整除的数有102,132,312共3个;
则被3整除的三位偶数的个数共有7个;
故X的可能取值有0,1,2;
X的分布列为
数学期望为EX=0×
+1×
+2×
=
.
| A | 3 5 |
| A | 2 4 |
个位数是0,
| A | 2 4 |
个位数是2,
| A | 2 4 |
| A | 1 3 |
个位数是5,
| A | 2 4 |
| A | 1 3 |
故三位数是偶数或能被5整除的数的概率为
| 12+9+9 |
| 48 |
| 5 |
| 8 |
(Ⅱ)由(Ⅰ)知,三位偶数共有21个,
个位数是0且能被3整除的数其十位数字与百位数字有(1,2),(1,5)排序,故共有4个;
个位数是2且能被3整除的数有102,132,312共3个;
则被3整除的三位偶数的个数共有7个;
故X的可能取值有0,1,2;
X的分布列为
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 4 |
| 9 |
| 4 |
| 9 |
| 1 |
| 9 |
| 2 |
| 3 |
点评:本题考查了概率的求法及分布列的列法和数学期望的求法,属于基础题.

练习册系列答案
 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
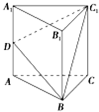 如图,在正三棱柱ABC A1B1C1中,D为棱AA1的中点,若截面三角形BC1D是面积为6的直角三角形,则此三棱柱的体积为( )
如图,在正三棱柱ABC A1B1C1中,D为棱AA1的中点,若截面三角形BC1D是面积为6的直角三角形,则此三棱柱的体积为( )A、16
| ||||
B、8
| ||||
C、4
| ||||
D、
|
 已知椭圆E:
已知椭圆E: