题目内容
已知函数f(x)=2cos2x―sin(2x―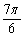 ).
).
(1)求函数f(x)的最大值,并写出f(x)取最大值时x的取值集合;
(2)已知△ABC中,角A, B, C的对边分别为a, b, c,若f(A)=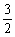 , b+c=2,求实数a的最小值。
, b+c=2,求实数a的最小值。
(1)f(x)=2cos2x-sin(2x-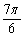 )=(1+cos2x)-(sin2xcos
)=(1+cos2x)-(sin2xcos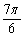 -cos2xsin
-cos2xsin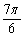 )
)
=1+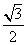 sin2x+
sin2x+ cos2x=sin(2x+
cos2x=sin(2x+ )+1 …………(3分)
)+1 …………(3分)
所以函数f(x)的最大值为2. …………(4分)
此时sin(2x+ )=1,即2x+
)=1,即2x+ =2kπ+
=2kπ+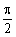 (k
(k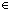 z) 解得x=kπ+
z) 解得x=kπ+ (k
(k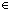 z)
z)
故x的取值集合为 {x| x=kπ+
{x| x=kπ+ ,k
,k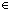 z} …………(6分)
z} …………(6分)
(2)由题意f(A)=sin(2A+ )+1=
)+1=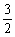 ,化简得sin(2A+
,化简得sin(2A+ )=
)= ,
,
∵A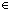 (0,π),
(0,π),  2A+
2A+
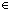 (
( ,
,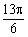 ).
).  A=
A=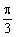 …………(8分)
…………(8分)
在三角形ABC中,根据余弦定理,
得a2=b2+c2-2bc·cos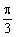 =(b+c)2-3bc …………(10分)
=(b+c)2-3bc …………(10分)
由b+c=2 知bc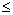 (
( )2=1, 即a2
)2=1, 即a2 1
1
 当b=c=1时,实数a的最小值为1. …………(12分)
当b=c=1时,实数a的最小值为1. …………(12分)

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 右支上的一点,M, N分别是圆(x+5)2+y2=4和
右支上的一点,M, N分别是圆(x+5)2+y2=4和 的图象大致为
的图象大致为

 B.
B.
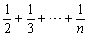 (n∈N*),经计算得f(4)>2, f(8)>
(n∈N*),经计算得f(4)>2, f(8)>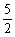 , f(16)>3, f(32)>
, f(16)>3, f(32)> ,
, 在x=0,x=
在x=0,x=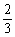 处存在极值。
处存在极值。 A.54cm2
A.54cm2  cm2
cm2  命题
命题 :“
:“ 中,若
中,若 则
则 。则下列命题为真命题的是 ( )
。则下列命题为真命题的是 ( ) B.
B. C.
C. D.
D.
 B.
B.  C.
C.  D.
D. 