题目内容
15.已知函数f(x)=|x+1|-|x-2|.(1)求不等式f(x)≥1的解集;
(2)若不等式f(x)≥x2-x+m的解集非空,求m的取值范围.
分析 (1)由于f(x)=|x+1|-|x-2|=$\left\{\begin{array}{l}{-3,x<-1}\\{2x-1,-1≤x≤2}\\{3,x>2}\end{array}\right.$,解不等式f(x)≥1可分-1≤x≤2与x>2两类讨论即可解得不等式f(x)≥1的解集;
(2)依题意可得m≤[f(x)-x2+x]max,设g(x)=f(x)-x2+x,分x≤1、-1<x<2、x≥2三类讨论,可求得g(x)max=$\frac{5}{4}$,从而可得m的取值范围.
解答 解:(1)∵f(x)=|x+1|-|x-2|=$\left\{\begin{array}{l}{-3,x<-1}\\{2x-1,-1≤x≤2}\\{3,x>2}\end{array}\right.$,f(x)≥1,
∴当-1≤x≤2时,2x-1≥1,解得1≤x≤2;
当x>2时,3≥1恒成立,故x>2;
综上,不等式f(x)≥1的解集为{x|x≥1}.
(2)原式等价于存在x∈R使得f(x)-x2+x≥m成立,
即m≤[f(x)-x2+x]max,设g(x)=f(x)-x2+x.
由(1)知,g(x)=$\left\{\begin{array}{l}{{-x}^{2}+x-3,x≤-1}\\{{-x}^{2}+3x-1,-1<x<2}\\{{-x}^{2}+x+3,x≥2}\end{array}\right.$,
当x≤-1时,g(x)=-x2+x-3,其开口向下,对称轴方程为x=$\frac{1}{2}$>-1,
∴g(x)≤g(-1)=-1-1-3=-5;
当-1<x<2时,g(x)=-x2+3x-1,其开口向下,对称轴方程为x=$\frac{3}{2}$∈(-1,2),
∴g(x)≤g($\frac{3}{2}$)=-$\frac{9}{4}$+$\frac{9}{2}$-1=$\frac{5}{4}$;
当x≥2时,g(x)=-x2+x+3,其开口向下,对称轴方程为x=$\frac{1}{2}$<2,
∴g(x)≤g(2)=-4+2+3=1;
综上,g(x)max=$\frac{5}{4}$,
∴m的取值范围为(-∞,$\frac{5}{4}$].
点评 本题考查绝对值不等式的解法,去掉绝对值符号是解决问题的关键,突出考查分类讨论思想与等价转化思想、函数与方程思想的综合运用,属于难题.

 阅读快车系列答案
阅读快车系列答案| A. | $\overrightarrow a=(1,-1,3),\overrightarrow n=(0,3,1)$ | B. | $\overrightarrow a=(1,0,0),\overrightarrow n=(-2,0,0)$ | ||
| C. | $\overrightarrow a=(0,2,1),\overrightarrow n=(-1,0,-1)$ | D. | $\overrightarrow a=(1,3,5),\overrightarrow n=(1,0,1)$ |
| A. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{10}$=1 | B. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1 |
| 最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
| 天数 | 2 | 16 | 36 | 25 | 7 | 4 |
(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
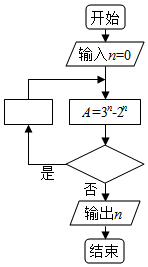 如图程序框图是为了求出满足3n-2n>1000的最小偶数n,那么在
如图程序框图是为了求出满足3n-2n>1000的最小偶数n,那么在 和
和 两个空白框中,可以分别填入( )
两个空白框中,可以分别填入( )| A. | A>1000和n=n+1 | B. | A>1000和n=n+2 | C. | A≤1000和n=n+1 | D. | A≤1000和n=n+2 |
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
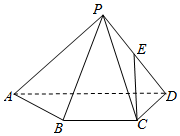 如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
如图,已知四棱锥P-ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.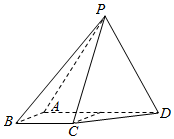 如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°.
如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=$\frac{1}{2}$AD,∠BAD=∠ABC=90°.