题目内容
16.函数y=x2+bx-4在(-∞,-1]上是减函数,在[-1,+∞)上是增函数,则( )| A. | b<0 | B. | b>0 | C. | b=0 | D. | b的符号不定 |
分析 由题意得出对称轴为x=-1,从而解出b=2.
解答 解:由题意得;
对称轴x=-$\frac{b}{2}$=-1,
解得:b=2>0,
故选B.
点评 本题考察了二次函数的性质问题,可结合图象一目了然,本题是基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
11.已知双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1的左焦点为F,点P为双曲线右支上一点,点A满足$\overrightarrow{AP}$•$\overrightarrow{AF}$=0,则点A到原点的最近距离为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
1.已知y=f(x)在定义域(-1,1)上是减函数,且f(1-a)<f(2a-1),则a的取值范围是( )
| A. | $a<\frac{2}{3}$ | B. | a>0 | C. | $0<a<\frac{2}{3}$ | D. | a<0或$a>\frac{2}{3}$ |
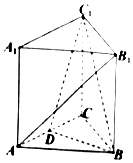 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,△ABC为正三角形,AA1=AB=6,点D为AC的中点.
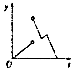
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,△ABC为正三角形,AA1=AB=6,点D为AC的中点. 如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t时时刻五角星露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S′(t)的图象大致为( )
如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t时时刻五角星露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S′(t)的图象大致为( )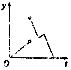
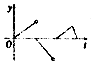
 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,过椭圆的焦点且与长轴垂直的弦长为1.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{3}}}{2}$,过椭圆的焦点且与长轴垂直的弦长为1.