题目内容
1.已知y=f(x)在定义域(-1,1)上是减函数,且f(1-a)<f(2a-1),则a的取值范围是( )| A. | $a<\frac{2}{3}$ | B. | a>0 | C. | $0<a<\frac{2}{3}$ | D. | a<0或$a>\frac{2}{3}$ |
分析 根据f(1-a)<f(2a-1),严格应用函数的单调性,要注意定义域.
解答 解:∵f(x)在定义域(-1,1)上是减函数,且f(1-a)<f(2a-1)
∴$\left\{\begin{array}{l}{-1<1-a<1}\\{-1<2a-1<1}\\{1-a>2a-1}\end{array}\right.$,∴0<a<$\frac{2}{3}$,
故选:C.
点评 本题主要考查应用单调性解题,一定要注意变量的取值范围.

练习册系列答案
相关题目
11.若cos θ=-$\frac{3}{5}$,且180°<θ<270°,则tan $\frac{θ}{2}$的值为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±$\frac{1}{2}$ |
16.函数y=x2+bx-4在(-∞,-1]上是减函数,在[-1,+∞)上是增函数,则( )
| A. | b<0 | B. | b>0 | C. | b=0 | D. | b的符号不定 |
6.设a=log54,b=log53,c=log45,则( )
| A. | a<c<b | B. | b<c<a | C. | a<b<c | D. | b<a<c |
10.函数y=(5x-3)3的导数是( )
| A. | y'=3(5x-3)2 | B. | y'=15(5x-3)2 | C. | y'=9(5x-3)2 | D. | y'=12(5x-3)2 |
10.设三条不同的直线l1,l2,l3满足l1⊥l3,l2⊥l3,则l1与l2( )
| A. | 是异面直线 | B. | 是相交直线 | ||
| C. | 是平行直线 | D. | 可能相交,或相交,或异面直线 |
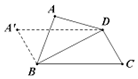 如图,矩形ABCD中,AB=1,BC=$\sqrt{3}$,将△ABD沿对角线BD向上翻折,若翻折过程中AC长度在[$\frac{\sqrt{10}}{2}$,$\frac{\sqrt{13}}{2}$]内变化,则点A所形成的运动轨迹的长度为$\frac{\sqrt{3}π}{12}$.
如图,矩形ABCD中,AB=1,BC=$\sqrt{3}$,将△ABD沿对角线BD向上翻折,若翻折过程中AC长度在[$\frac{\sqrt{10}}{2}$,$\frac{\sqrt{13}}{2}$]内变化,则点A所形成的运动轨迹的长度为$\frac{\sqrt{3}π}{12}$.