题目内容
3.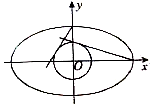 如图,过椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>1)上顶点和右顶点分别作圆x2+y2=1的两条切线的斜率之积为-$\frac{{\sqrt{2}}}{2}$,则椭圆的离心率的取值范围是$({0,\frac{{\sqrt{2}}}{2}})$.
如图,过椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>1)上顶点和右顶点分别作圆x2+y2=1的两条切线的斜率之积为-$\frac{{\sqrt{2}}}{2}$,则椭圆的离心率的取值范围是$({0,\frac{{\sqrt{2}}}{2}})$.
分析 由题意设出两切线方程,由点到直线的距离公式可得a与k,b与k的关系,代入椭圆离心率可得e与k的关系,求出函数值域得答案.
解答 解:由题意设两条切线分别为:y=kx+b,y=-$\frac{\sqrt{2}}{2k}$(x-a)(k≠0),
由圆心到两直线的距离均为半径得:
$\frac{b}{\sqrt{{k}^{2}+1}}=1$,$\frac{\sqrt{2}a}{\sqrt{4{k}^{2}+2}}=1$,
化简得:b2=k2+1,a2=2k2+1.
∴$e=\frac{c}{a}=\sqrt{\frac{{c}^{2}}{{a}^{2}}}=\sqrt{\frac{{a}^{2}-{b}^{2}}{{a}^{2}}}=\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{1-\frac{{k}^{2}+1}{2{k}^{2}+1}}$
=$\sqrt{\frac{1}{2+\frac{1}{{k}^{2}}}}$(k≠0).
∴0<e<$\frac{\sqrt{2}}{2}$.
故答案为:$({0,\frac{{\sqrt{2}}}{2}})$.
点评 本题考查椭圆的简单性质,考查了点到直线距离公式的应用,训练了函数值域的求法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.若六棱柱ABCDEF-A1B1C1D1E1F1的底面是边长为1的正六边形,侧棱AA1⊥底面ABCDEF,且$A{A_1}=\sqrt{6}$,则异面直线EF与BD1所成的角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
18.已知实数x,y满足$\left\{\begin{array}{l}y≤1\\ y≥2x-1\\ x+y≥m\end{array}\right.$如果目标函数z=y-x的最小值为-2,则实数m等于( )
| A. | 0 | B. | -2 | C. | -4 | D. | 1 |
15.要得到函数y=sin2x的图象,只要将函数y=sin(2x+$\frac{π}{3}$)的图象( )
| A. | 向左平移$\frac{π}{6}$单位即可 | B. | 向右平移$\frac{π}{6}$单位即可 | ||
| C. | 向右平移$\frac{π}{3}$单位即可 | D. | 向左平移$\frac{π}{3}$单位即可 |
12.已知实数a,b满足2a=3,3b=2,则函数f(x)=ax+x-b的零点个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |