题目内容
证明: .
.
 .
.数学归纳法或用放缩再拆项相消法.
试题分析:(ⅰ)当n=1时,
 ,
, ,
, 2分
2分(ⅱ)假设当n=k时,
 4分
4分则当n=k+1时,

要证:

只需证:

由于

所以
 11分
11分于是对于一切的自然数
 ,都有
,都有 12分
12分此题也可以用放缩再拆项相消法.
点评:中档题,本题解法较为灵活,可采用数学归纳法,也可以先放缩,再利用数列求和方法“裂项相消法”。总之,不等式证明中,“放缩”思想是常用的一中思想方法。

练习册系列答案
相关题目
 是关于
是关于 的方程
的方程
 的根,
的根, ;(Ⅱ)
;(Ⅱ) .
. -1,证明:
-1,证明: (x-1);
(x-1); .
.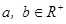 ,试证:
,试证: ;并求函数
;并求函数 (
( )的最小值.
)的最小值. ,证明:
,证明: .
.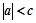
 ,求证:
,求证: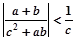 .
.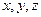 均为正数,
均为正数, ,则
,则 的最小值是 ( )
的最小值是 ( )


