题目内容
1．计算定积分（1）${∫}_{-1}^{1}$（x2+cosx）dx
（2）${∫}_{-2}^{2}$$（x+\sqrt{4-{x^2}}）dx}$．
分析 求出原函数，即可求出定积分．
解答 解：（1）${∫}_{-1}^{1}$（x2+cosx）dx=（$\frac{1}{3}{x}^{3}+sinx$）${|}_{-1}^{1}$=$\frac{2}{3}$+2sin1；
（2）${∫}_{-2}^{2}$$（x+\sqrt{4-{x^2}}）dx}$=$\frac{1}{2}{x}^{2}{|}_{-2}^{2}$+${∫}_{-2}^{2}\sqrt{4-{x}^{2}}dx$=2π．
点评 本题考查定积分知识，考查学生的计算能力，确定原函数是关键．
练习册系列答案
相关题目
11．设函数$f（x）=x-\frac{1}{x}$，对任意x∈[1，+∞），f（mx）+mf（x）＜0恒成立，则实数m的取值范围是 （ ）
| A． | m＜-1或0＜m＜1 | B． | 0＜m＜1 | C． | m＜-1 | D． | -1＜m＜0 |
12．若$α∈（0，\frac{π}{2}）$，若$cos（α+\frac{π}{6}）=\frac{4}{5}$，则$sin（2α+\frac{π}{3}）$的值为（ ）
| A． | $\frac{12}{25}$ | B． | $\frac{24}{25}$ | C． | $-\frac{24}{25}$ | D． | $-\frac{12}{25}$ |
6．下列有关命题的说法正确的是（ ）
| A． | 命题“若x2=1，则x=1”的否命题为：“若x2=1，则x≠1” | |
| B． | “x=-1”是“x2-5x-6=0”的必要不充分条件 | |
| C． | 命题“?x∈R，使得x2+x+1＜0”的否定是：“?x∈R，均有x2+x+1＜0” | |
| D． | 命题“若x＞1，则$\frac{1}{x}$＜1”的逆否命题为真命题 |
10．一个袋中装有大小相同的5个白球和3个红球，现在不放回的取2次球，每次取出一个球，记“第1次拿出的是白球”为事件A，“第2次拿出的是白球”为事件B，则P（B|A）是（ ）
| A． | $\frac{5}{8}$ | B． | $\frac{5}{16}$ | C． | $\frac{4}{7}$ | D． | $\frac{5}{14}$ |
11．
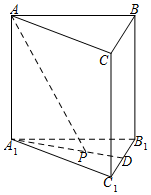已知正三棱柱（底面是正三角形，且侧棱与底面垂直的棱柱）ABC-A1B1C1体积为$\frac{9}{4}$，底面边长为$\sqrt{3}$．若P为底面A1B1C1的中心，则PA与平面ABC所成角的大小为（ ）
已知正三棱柱（底面是正三角形，且侧棱与底面垂直的棱柱）ABC-A1B1C1体积为$\frac{9}{4}$，底面边长为$\sqrt{3}$．若P为底面A1B1C1的中心，则PA与平面ABC所成角的大小为（ ）| A． | $\frac{π}{2}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{6}$ |