题目内容
14．如图所示，使电路接通，开关不同的开闭方式共有（ ）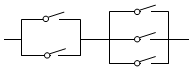
| A． | 11 | B． | 12 | C． | 20 | D． | 21 |
分析 设5个开关依次为1、2、3、4、5，由电路知识分析可得电路接通，则开关1、2与3、4、5中至少有1个接通，依次分析开关1、2与3、4、5中至少有1个接通的情况数目，由分步计数原理，计算可得答案．
解答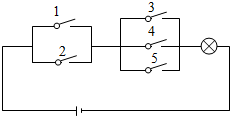 
解：根据题意，设5个开关依次为1、2、3、4、5，
若电路接通，则开关1、2与3、4、5中至少有1个接通，
对于开关1、2，共有2×2=4种情况，其中全部断开的有1种情况，则其至少有1个接通的有4-1=3种情况，
对于开关3、4、5，共有2×2×2=8种情况，其中全部断开的有1种情况，则其至少有1个接通的8-1=7种情况，
则电路接通的情况有3×7=21种；
故选：D．
点评 本题考查分步计数原理的应用，可以用间接法分析开关至少有一个闭合的情况，关键是分析出电路解题的条件．
练习册系列答案
相关题目
如图，在三棱锥A-BCD中，AB⊥平面BCD，BC⊥BD，BC=3，BD=4，直线AD与平面BCD所成的角为45°，点E，F分别是AC，AD的中点．
5．某商场举行优惠促销活动，顾客仅可以从以下两种优惠方案中选择一种，
方案一：每满200元减50元：
方案二：每满200元可抽奖一次．具体规则是依次从装有3个红球、1个白球的甲箱，装有2个红球、2个白球的乙箱，以及装有1个红球、3个白球的丙箱中各随机摸出1个球，所得结果和享受的优惠如下表：（注：所有小球仅颜色有区别）
（Ⅰ）若两个顾客都选择方案二，各抽奖一次，求至少一个人获得半价优惠的概率；
（Ⅱ）若某顾客购物金额为320元，用所学概率知识比较哪一种方案更划算？
方案一：每满200元减50元：
方案二：每满200元可抽奖一次．具体规则是依次从装有3个红球、1个白球的甲箱，装有2个红球、2个白球的乙箱，以及装有1个红球、3个白球的丙箱中各随机摸出1个球，所得结果和享受的优惠如下表：（注：所有小球仅颜色有区别）
| 红球个数 | 3 | 2 | 1 | 0 |
| 实际付款 | 半价 | 7折 | 8折 | 原价 |
（Ⅱ）若某顾客购物金额为320元，用所学概率知识比较哪一种方案更划算？
2．已知f（x）是定义域为R的偶函数，且当x≥0时，f（x）=（$\frac{1}{2}$）x，则不等式f（x）＞$\frac{1}{2}$的解集为（ ）
| A． | （-$\frac{1}{4}$，$\frac{1}{4}$） | B． | （-$\frac{1}{2}$，$\frac{1}{2}$） | C． | （-2，2） | D． | （-1，1） |
9．已知函数f（x）=x3-ax2+4，若f（x）的图象与x轴正半轴有两个不同的交点，则实数a的取值范围为（ ）
| A． | （1，+∞） | B． | （$\frac{3}{2}$，+∞） | C． | （2，+∞） | D． | （3，+∞） |
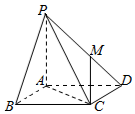如图，在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，PA⊥底面ABCD，PA=AB，点M在棱PD上，PB∥平面ACM．