题目内容

已知函数y=
2k
k2+1
，求当k≥0时该函数的最小值．
考点：基本不等式在最值问题中的应用
专题：计算题,函数的性质及应用,不等式的解法及应用
分析：利用观察法可直接写出最小值．
解答： 解：y=
2k
k2+1
≥0，
且当k=0时，y=0；
故该函数的最小值为0．
点评：本题考查了函数的最值的求法，注意到分子分母都不是负数，从而求解．
练习册系列答案
相关题目
已知f（x）=
xlnx
1+x
，在x=x0处取得极值．
（1）证明：f（x0）=-x0；
（2）是否存在实数a，使得对任意x∈（0，+∞），f（x）≥
a(x-1)
x
？若存在，求a的所有值；若不存在，说明理由．
已知双曲线左右焦点分别为F1，F2，点P为其右支上的一点∠F1PF2=60°，且S△F1PF2=
23
，若|PF1|，
1
4
|F1F2|2，|PF2|成等差数列，则该双曲线的离心率（　　）
A、
3
B、2
3
C、2
D、
2
已知一条直线l过定点M（2，1），且与x，y轴的正半轴分别相交于A，B（O是直角坐标系的原点）．
（1）当三角形△ABO的面积为
9
2
时，求直线l的方程；
（2）当三角形△ABO的面积最小时，求直线l的方程．
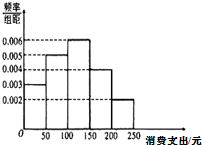已知100名学生某月饮料消费支出情况的频率分布直方图如图所示．则这100名学生中，该月饮料消费支出超过150元的人数是
 
．
①正相关，②负相关，③不相关，则下列散点图分别反映的变量是（　　）
A、①②③B、②③①
C、②①③D、①③②
已知数列{an}的前n项和记为Sn，a1=2，an+1=Sn+n．
（1）求{an}的通项公式；
（2）等差数列{bn}的各项为正，其前n项和为Tn，且T3=9，又a1+b1，a2+b2，a3+b3成等比数列，
①求{bn}的通项公式；
②求证：当n≥2时，
1
b12
+
1
b22
+…+
1
bn2
＜
5
4
．
已知函数f（x）=
3x-1，x≤1
1+log2xx＞1
，则函数f（x）的零点为（　　）
A、
1
2
，0
B、-2，0
C、C、
1
2
D、0
已知圆C：x2+y2-2x-4y+m=0．
（1）求m的取值范围．
（2）当m=4时，若圆C与直线x+ay-4=0交于M，N两点，且
CM
⊥
CN
，求a的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网