题目内容
设集合A{x|-1≤x<3},B={x|42x-4≥4x-2},C={x|x≥a-1}.
(1)求A∩(∁RB);
(2)若B∪C=C,求实数a的取值范围.
(1)求A∩(∁RB);
(2)若B∪C=C,求实数a的取值范围.
考点:交、并、补集的混合运算
专题:集合
分析:(1)求出B中不等式的解集确定出B,求出B的补集,找出A与B补集的交集即可;
(2)根据B与C并集为C,求出a的范围即可.
(2)根据B与C并集为C,求出a的范围即可.
解答:
解:(1)由B中不等式变形得:2x-4≥x-2,即x≥2,
∴B={x|x≥2},
∵∁RB={x|x<2},
∴A∩(∁RB)={x|-1≤x<2};
(2)∵B={x|x≥2},C={x|x≥a-1},且B∪C=C,
∴B⊆C,
∴a-1≤2,即a≤3,
则实数a的范围是{a|a≤3}.
∴B={x|x≥2},
∵∁RB={x|x<2},
∴A∩(∁RB)={x|-1≤x<2};
(2)∵B={x|x≥2},C={x|x≥a-1},且B∪C=C,
∴B⊆C,
∴a-1≤2,即a≤3,
则实数a的范围是{a|a≤3}.
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
平面向量
与
的夹角为
,
=(3,0),|
|=2,则|
+2
|═( )
| a |
| b |
| 2π |
| 3 |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
| C、7 | ||
| D、3 |
已知全集M={x||2x-1|≤1,x∈Z},集合N={3,a},若M∩N≠∅,则a等于( )
| A、1 | B、2 | C、1或2 | D、0或1 |
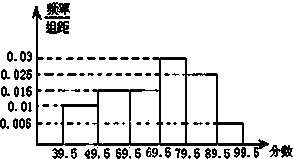 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
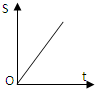
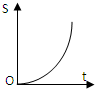
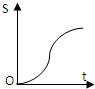
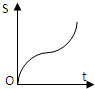
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题: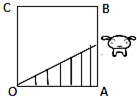 如图,正方形街道OABC,已知小白从A出发,沿着正方形边缘A-B-C匀速走动,小白与O连线扫过的正方形内阴影部分面积S是时间t的函数,这个函数的大致图象是( )
如图,正方形街道OABC,已知小白从A出发,沿着正方形边缘A-B-C匀速走动,小白与O连线扫过的正方形内阴影部分面积S是时间t的函数,这个函数的大致图象是( )