题目内容
17.已知数列{an}为等比数列,满足a4+a7=2,a2•a9=-8,则a1+a13的值为( )| A. | 7 | B. | 17 | C. | -$\frac{17}{2}$ | D. | 17或-$\frac{17}{2}$ |
分析 由已知结合等比数列的性质可知a5•a6=a4•a7,从而可求a4,a7,进而可求q3、a1,即可得出结论.
解答 解:a4+a7=2,a2•a9=-8,由等比数列的性质可知a2•a9=a4•a7
∴a4•a7=-8,a4+a7=2,
∴a4=-2,a7=4或a4=4,a7=-2,
∴a1=1,q3=-2或a1=-8,q3=-$\frac{1}{2}$,
∴a1+a13=1+16=17或a1+a13=-8-$\frac{1}{2}$=-$\frac{17}{2}$.
故选:D.
点评 本题主要考查了等比数列的通项公式及等比数列的性质的简单应用,属于基础试题.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
8.若sinα=$\frac{k+1}{k-3}$,cosα=$\frac{k-1}{k-3}$,则$\frac{1}{tanα}$的值为( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
9.执行如图所示程序框图,若使输出的结果不大于50,则输入的整数k的最大值为( )
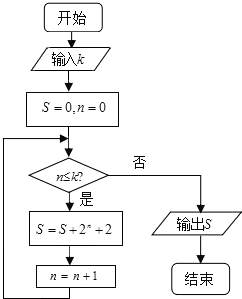

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |