题目内容
若函数y=
的定义域为实数集R，求实数a的取值范围．
| 1 | ||
|
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：依据题意可得：函数的定义域为R的等价条件是ax2-2ax+a+1＞0，对?x∈R恒成立，由此可得a=0或
从而求出a的范围．
|
解答：
解：∵函数y=
的定义域为实数集R，
∴ax2-2ax+a+1＞0，对?x∈R恒成立，
∴a=0或
即：a≥0．
| 1 | ||
|
∴ax2-2ax+a+1＞0，对?x∈R恒成立，
∴a=0或
|
即：a≥0．
点评：本题考查了函数的定义域为R的条件及函数与方程的关系，利用一元二次函数的图象分析一元二次不等式的解集是解答此类问题的常用方法．
练习册系列答案
相关题目
命题“所有能被3整除的整数都是奇数”的否定是（ ）
| A、所有不能被3整除的整数都是奇数 |
| B、所有能被3整除的整数都不是奇数 |
| C、存在一个不能被3整除的整数是奇数 |
| D、存在一个能被3整除的整数不是奇数 |
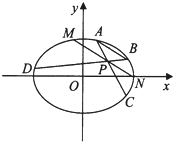如图所示，离心率为