题目内容
用反证法证明：圆的两条不是直径的相交弦不能互相平分．
考点：反证法与放缩法
专题：反证法
分析：利用反证法假设圆的两条不是直径的相交弦能互相平分，推出矛盾即可．
解答：
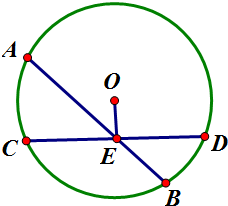证法一：假设圆的两条不是直径的相交弦能互相平分，
如图AB，CD为圆O的两条不是直径且互相平分的相交弦，交点为E
∵CE=DE，AE=BE，O为圆心
∴OE⊥CD，OE⊥AB
∴CD∥AB
显然与AB，CD矛盾，故假设不成立．
∴圆的两条不是直径的相交弦不能互相平分．
证法二：证明：假设AB，CD能互相平分
连接OE
∵AE=BE
∴OE⊥AB
同理OE⊥CD
因为这与过一点有且有一条直线与已知直线垂直相矛盾，所以假设错误，所以圆的两条不是直径的相交弦不能互相平分．
证法一：假设圆的两条不是直径的相交弦能互相平分，如图AB，CD为圆O的两条不是直径且互相平分的相交弦，交点为E
∵CE=DE，AE=BE，O为圆心
∴OE⊥CD，OE⊥AB
∴CD∥AB
显然与AB，CD矛盾，故假设不成立．
∴圆的两条不是直径的相交弦不能互相平分．
证法二：证明：假设AB，CD能互相平分
连接OE
∵AE=BE
∴OE⊥AB
同理OE⊥CD
因为这与过一点有且有一条直线与已知直线垂直相矛盾，所以假设错误，所以圆的两条不是直径的相交弦不能互相平分．
点评：本题主要考察了反证法，以及圆的相关知识，属于基础题．
练习册系列答案
优学名师名题系列答案
相关题目
已知数列{an}中，a1=3，an+1=2an+1，则a3=（ ）
| A、3 | B、7 | C、15 | D、18 |
奇函数f（x）在（0，+∞）上为减函数，且f（3）=0，则不等式
＞0的解集为（ ）
| f(x)-f(-x) |
| 3x |
| A、（-∞，3）∪（3，+∞） |
| B、（-3，0）∪（0，3） |
| C、（-3，3） |
| D、（3，+∞） |