Question

20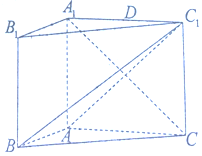．如图，在三棱柱ABC-A₁B₁C₁中，侧面ABB₁A₁是矩形，∠BAC=90°，AA₁⊥BC，AA₁=AC=2AB=4，且BC₁⊥A₁C
（1）求证：平面ABC₁⊥平面A₁ACC₁
（2）设D是A₁C₁的中点，判断并证明在线段BB₁上是否存在点E，使DE∥平面ABC₁，若存在，求点E到平面ABC₁的距离．

Answer 1

分析 （1）在三棱柱ABC-A₁B₁C₁中，由侧面ABB₁A₁是矩形，可得AA₁⊥AB，又AA₁⊥BC，可得AA₁⊥平面ABC，得到AA₁⊥AC，进一步有A₁C⊥AC₁，结合BC₁⊥A₁C，可得A₁C⊥平面ABC₁，由面面垂直的判定得平面ABC₁⊥平面A₁ACC₁ ；
（2）当E为BB₁的中点时，连接AE，EC₁，DE，取AA₁的中点F，连接EF，FD，由面面平行的判定和性质可得DE∥平面ABC₁，咋爱优等体积法可求点E到平面ABC₁的距离为．

解答 （1）证明：在三棱柱ABC-A₁B₁C₁中，侧面ABB₁A₁是矩形，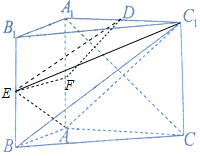
∴AA₁⊥AB，又AA₁⊥BC，AB∩BC=B，
∴AA₁⊥平面ABC，
∴AA₁⊥AC，又AA₁=AC，∴A₁C⊥AC₁，
又BC₁⊥A₁C，BC₁∩AC₁=C₁，
∴A₁C⊥平面ABC₁，又A₁C?平面A₁ACC₁，
∴平面ABC₁⊥平面A₁ACC₁ ；
（2）解：当E为BB₁的中点时，连接AE，EC₁，DE，
如图，取AA₁的中点F，连接EF，FD，
∵EF∥AB，DF∥AC₁，
又EF∩DF=F，AB∩AC₁=A，
∴平面EFD∥平面ABC₁，又DE?平面EFD，
∴DE∥平面ABC₁，
又∵${V}_{E-AB{C}_{1}}={V}_{{C}_{1}-ABE}$，C₁A₁⊥平面ABE，
设点E到平面ABC₁ 的距离为d，
∴$\frac{1}{3}×\frac{1}{2}×2×4\sqrt{2}×d=\frac{1}{3}×\frac{1}{2}×2×2×4$，得d=$\sqrt{2}$，
∴点E到平面ABC₁的距离为$\sqrt{2}$．

点评 本题考查平面与平面垂直的判定，考查了空间想象能力和思维能力，训练了利用等积法求多面体的体积，是中档题．