题目内容
12. 如图所示,在三棱锥P-ABC中,PA⊥底面ABC,D是PC的中点. 已知∠BAC=$\frac{π}{2}$,AB=2,AC=2,PA=2.求:
如图所示,在三棱锥P-ABC中,PA⊥底面ABC,D是PC的中点. 已知∠BAC=$\frac{π}{2}$,AB=2,AC=2,PA=2.求:(1)三棱锥P-ABC的体积;
(2)异面直线BC与AD所成角的余弦值.
分析 (1)先求出△ABC的面积,由此能求出三棱锥P-ABC的体积.
(2)取PB的中点E,连接DE,AE,则ED∥BC,∠ADE是异面直线BC与AD所成的角(或其补角).由此能求出异面直线BC与AD所成角的余弦值.
解答 解:(1)∵在三棱锥P-ABC中,PA⊥底面ABC,D是PC的中点. 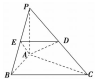
∠BAC=$\frac{π}{2}$,AB=2,AC=2,PA=2.
∴${S}_{△ABC}=\frac{1}{2}×2×2=2$,
∴三棱锥P-ABC的体积为V=$\frac{1}{3}{S}_{△ABC}•PA=\frac{1}{3}×2×2=\frac{4}{3}$.
(2)如图,取PB的中点E,连接DE,AE,则ED∥BC,
∴∠ADE是异面直线BC与AD所成的角(或其补角).
在△ADE中,DE=$\sqrt{2}$,AE=$\sqrt{2}$,AD=$\sqrt{2}$,
cos$∠ADE=\frac{D{E}^{2}+A{D}^{2}-A{E}^{2}}{2DE•AD}$=$\frac{1}{2}$,
故异面直线BC与AD所成角的余弦值为$\frac{1}{2}$.
点评 本题考查三棱锥的体积的求法,考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
2.在空间直角坐标系中,在z轴上的点的坐标可记为( )
| A. | (0,b,0) | B. | (a,0,0) | C. | (0,0,c) | D. | (0,b,c) |
7.已知函数 f(x)=$\left\{\begin{array}{l}{-2x(-1≤x≤0)}\\{\sqrt{x}(0<x≤1)}\end{array}\right.$,则下列图象正确的是( )
| A. | 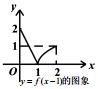 | B. | 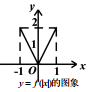 | C. | 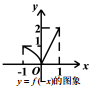 | D. | 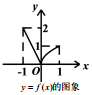 |
1.设向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$=(1,2),$\overrightarrow{a}•\overrightarrow{b}$=-5,$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影是( )
| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | -$\sqrt{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
11.对任意的实数k,直线y=kx+$\sqrt{3}$与圆x2+y2=4的位置关系一定是( )
| A. | 相离 | B. | 相交但直线过圆心 | ||
| C. | 相切 | D. | 相交但直线不过圆心 |
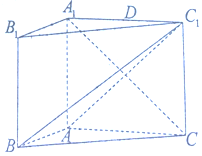 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1是矩形,∠BAC=90°,AA1⊥BC,AA1=AC=2AB=4,且BC1⊥A1C
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1是矩形,∠BAC=90°,AA1⊥BC,AA1=AC=2AB=4,且BC1⊥A1C