题目内容
5．若函数 y=$\frac{x-m}{x-1}$在区间 （1，+∞）内是减函数，则实数m的取值范围是m＜1．分析 若函数 y=$\frac{x-m}{x-1}$在区间 （1，+∞）内是减函数，则y′=$\frac{m-1}{（x-1）^{2}}$＜0恒成立，解得答案．
解答 解：若函数 y=$\frac{x-m}{x-1}$在区间 （1，+∞）内是减函数，
y′=$\frac{m-1}{（x-1）^{2}}$＜0恒成立，
即m-1＜0，
解得：m＜1，
故答案为：m＜1
点评 本题考查的知识点是利用导数研究函数的单调性，难度不大，属于中档题．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
15．某几何体的三视图如图所示，则该几何体的外接球的表面积为（ ）
| A． | 24π | B． | 12π | C． | 8π | D． | 6π |
16．某花店每天以每枝5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售，如果当天卖不完，剩下的玫瑰花作垃圾处理．花店记录了100天玫瑰花的日需求量（单位：枝），整理得下表：
以100天记录的各需求量的频数作为各需求量发生的概率．
（1）若花店一天购进16枝玫瑰花，X表示当天的利润（单位：元），求X的分布列、数学期望及方差；
（2）若花店计划一天购进16枝或17枝玫瑰花，你认为应购进16枝还是17枝？说明理由．
| 日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
（1）若花店一天购进16枝玫瑰花，X表示当天的利润（单位：元），求X的分布列、数学期望及方差；
（2）若花店计划一天购进16枝或17枝玫瑰花，你认为应购进16枝还是17枝？说明理由．
13．设函数f（x）=$\frac{2^x}{{1+{2^x}}}-\frac{1}{2}$，[x]表示不超过x的最大整数，则函数y=[f（x）]的值域为（ ）
| A． | {0} | B． | {-1，0} | C． | {-1，0，1} | D． | {-2，0} |
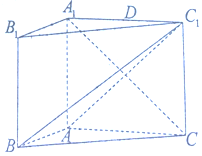如图，在三棱柱ABC-A1B1C1中，侧面ABB1A1是矩形，∠BAC=90°，AA1⊥BC，AA1=AC=2AB=4，且BC1⊥A1C